Exercise Sheet 4 : problem 2

Question

Given a FSM: A={2Vin,2Vout,I,2Vstate,R}A={2Vin,2Vout,I,2Vstate,R}
where Vin={a}Vin={a}, Vout={o}Vout={o}, Vstate={p,q}Vstate={p,q}, I=I=q,
R=R=(next(q)|q|p)&!(o->a)&next(p)

a)

• label 0:; 1:p; 2:q; 3:p,q;
      i.e., node s0-s3 represent states !p&!q, p&!q, !p&q and p&q, respectively.
• inputs {a},{};
      i.e., two inputs represent a and !a, respectively.
• outputs {o},{};
      i.e., two outputs represent o and !o, respectively.

After computing the DNF of  midterms of transition relation, I got the following representation:

p ^ q ^ o ^ !a ^ !next(q) ^ next(p) v

p ^ q ^ o ^ !a ^ next(q) ^ next(p) v

p ^ !q ^ o ^ !a ^ !next(q) ^ next(p) v

p ^ !q ^ o ^ !a ^ next(q) ^ next(p) v

!p ^ q ^ o ^ !a ^ !next(q) ^ next(p) v

!p ^ q ^ o ^ !a ^ next(q) ^ next(p) 

Therefore, I get this transition:

{p,q} ---- 0&!a --- {p}

{p,q} ---- 0&!a --- {p,q}

{p} ---- 0&!a --- {p}

{p} ---- 0&!a --- {p,q}

{q} ---- 0&!a --- {p}

{q} ---- 0&!a --- {p,q}

I got the below diagram:

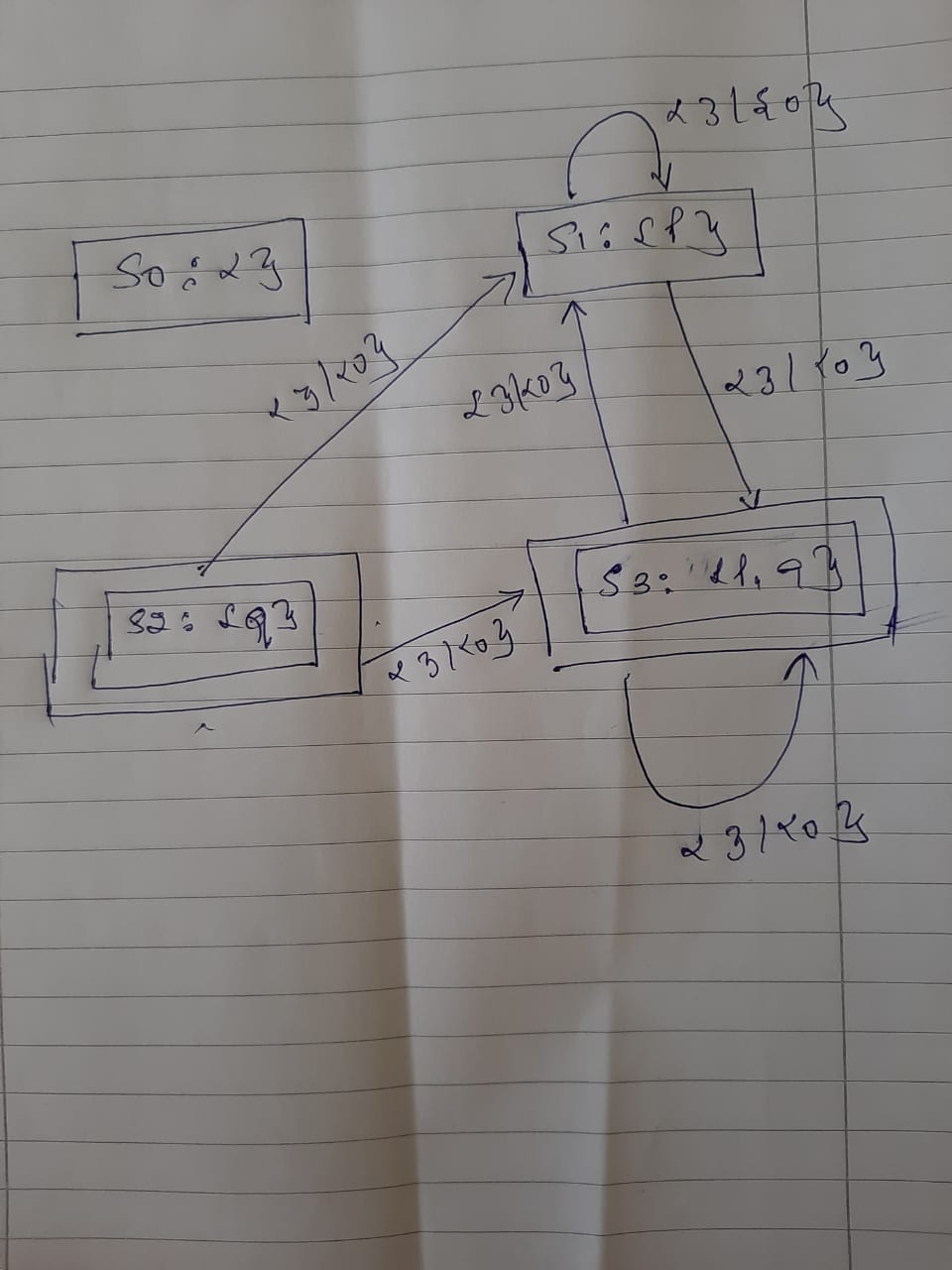
Below is my answer:

init 2,3;

transitions (1,{},{o},1); (1,{},{o},3); (2,{},{o},1); (2,{},{o},3); (3,{},{o},1); (3,{},{o},3);

It says answer is wrong in the tool.

Not sure which part I have done wrong. can anyone help me on this?

Comments

I incorrectly posted my answer as a comment first and can't delete it, see below for the answer.

Answer 1

From what I calculated, there is a missing minterm in the DNF !p&!q&!a&o&next(p)&next(q). In your FSM there is only a transition missing from s0 to s3. The other part that you have written is correct. You can also check if you FSM is correct with the online tool, just to be sure no transitions or states are missing.

Answer 2

(next(q)|q|p)&!(o->a)&next(p)
= (next(q)|q|p)&o&!a&next(p)
= next(q)&o&!a&next(p)|q&o&!a&next(p)|p&o&!a&next(p)

Now, you need to find the transitions satisfying one of those assignments:
next(q)&o&!a&next(p)
q&o&!a&next(p)
p&o&!a&next(p)

These are:
{} ---- 0&!a --- {p,q}
{p} ---- 0&!a --- {p,q}
{q} ---- 0&!a --- {p,q}
{p,q} ---- 0&!a --- {p,q}
(first term)

{q} ---- 0&!a --- {p}
{q} ---- 0&!a --- {p,q} (however, this is a duplicate)
{p,q} ---- 0&!a --- {p}
{p,q} ---- 0&!a --- {p,q} (duplicate)
(second term)

{p} ---- 0&!a --- {p}
{p} ---- 0&!a --- {p,q} (duplicate)
{p,q} ---- 0&!a --- {p} (duplicate)
{p,q} ---- 0&!a --- {p,q} (duplicate)

It seems that you forgot {} ---- 0&!a --- {p,q} in your solution.