Exercise 4 Qn 2: FSM to Kripke Structure invalid answers

Question

Given a FSM: A={2Vin,2Vout,I,2Vstate,R}A={2Vin,2Vout,I,2Vstate,R}
where Vin={a}, Vout={o}, Vstate={p,q}

I=!(q<->p),

R=(next(q)|p->!(o->a))&q&next(p)

I am trying to compute the deadends, initial states, reachable states for the following FSM and i get the following:

But the system is not accepting my answers. I tried to compute with the help of tool and it matches with my calculation. Can anybody please tell me where am I making mistake!!!! :(

Answer 1

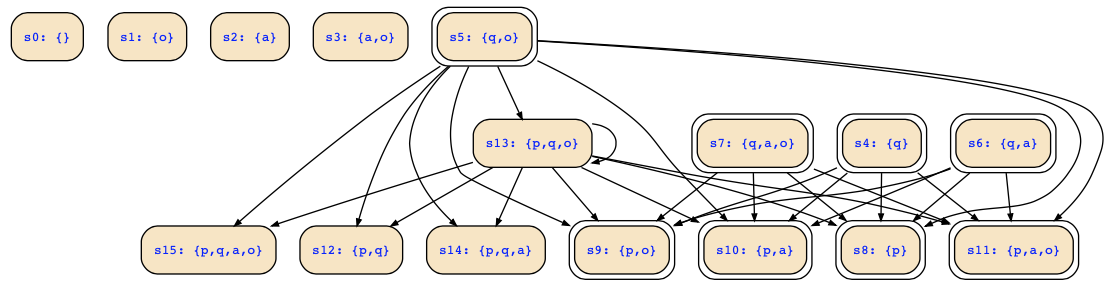
We consider a Kripke structure with variables p,q,a,o, initial states I=¬(q<->p) and transition relation R=(next(q) ∨ p->¬(o->a)) ∧ q ∧ next(p). The state transition system looks as follows:

The transition relation can be simplified to 

   q ∧ ¬a ∧ o ∧ next(p) ∨ ¬p ∧ q ∧ next(p) ∧ ¬next(q)

The deadend states, i.e., states without outgoing transitions, are computed as pre∀(false) which is computed as ¬(q ∧ ¬(o->a)) ∧ ¬(q ∧ (p->¬(o->a))) and can be simplified as p ∧ ¬o ∨ ¬q ∨ p ∧ a. If you expand it to a full DNF, you see the following eleven states:

    ¬p ∧ ¬q ∧ ¬a ∧ ¬o ∨ 
    ¬p ∧ ¬q ∧  a ∧ ¬o ∨ 
    ¬p ∧ ¬q ∧ ¬a ∧  o ∨ 
     p ∧  q ∧  a ∧  o ∨ 
     p ∧  q ∧  a ∧ ¬o ∨ 
     p ∧  q ∧ ¬a ∧ ¬o ∨ 
     p ∧ ¬q ∧  a ∧  o ∨ 
     p ∧ ¬q ∧  a ∧ ¬o ∨ 
     p ∧ ¬q ∧ ¬a ∧  o ∨ 
     p ∧ ¬q ∧ ¬a ∧ ¬o ∨ 
    ¬p ∧ ¬q ∧  a ∧  o

To remove transitions leading to them, we modify the transition relation to

      (q ∧ ¬a ∧ o ∧ next(p) ∨ ¬p ∧ q ∧ next(p) ∧ ¬next(q))  
    ∧  
      ¬(next(p) ∧ ¬next(o) ∨ ¬next(q) ∨ next(p) ∧ next(a))

Left are now just the following transitions (I don't show the other 14 states without transitions):

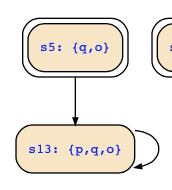
I guess the solution should just consider this clean-up of the structure, i.e., the structure reduced to states on infinite paths. From here, it should be simple to get the final answers. 

Comments

Thanks for your reply! I can see my answers are matching with your answer. But still the system is showing it as wrong. Can you please check my answers and point out my mistake? Thanks..

---

As said, I think that you should consider the cleaned Kripke structure with the remaining two states. Then, there would be only one initial state, and only two reachable states.

---

Got it. Thanks!