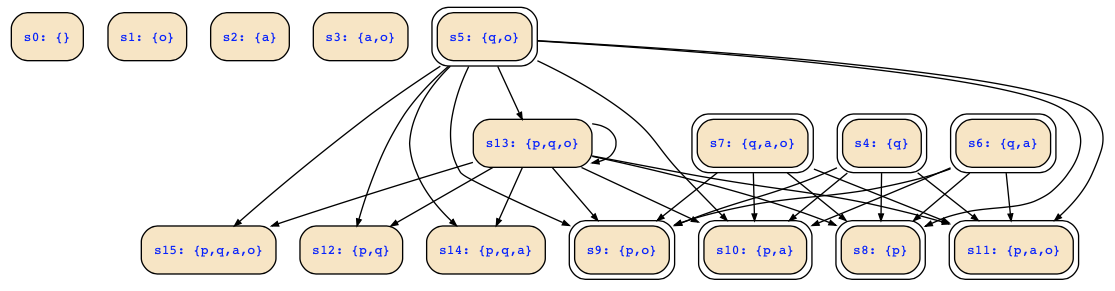
We consider a Kripke structure with variables p,q,a,o, initial states I=¬(q<->p) and transition relation R=(next(q) ∨ p->¬(o->a)) ∧ q ∧ next(p). The state transition system looks as follows:
The transition relation can be simplified to
q ∧ ¬a ∧ o ∧ next(p) ∨ ¬p ∧ q ∧ next(p) ∧ ¬next(q)
The deadend states, i.e., states without outgoing transitions, are computed as pre∀(false) which is computed as ¬(q ∧ ¬(o->a)) ∧ ¬(q ∧ (p->¬(o->a))) and can be simplified as p ∧ ¬o ∨ ¬q ∨ p ∧ a. If you expand it to a full DNF, you see the following eleven states:
¬p ∧ ¬q ∧ ¬a ∧ ¬o ∨
¬p ∧ ¬q ∧ a ∧ ¬o ∨
¬p ∧ ¬q ∧ ¬a ∧ o ∨
p ∧ q ∧ a ∧ o ∨
p ∧ q ∧ a ∧ ¬o ∨
p ∧ q ∧ ¬a ∧ ¬o ∨
p ∧ ¬q ∧ a ∧ o ∨
p ∧ ¬q ∧ a ∧ ¬o ∨
p ∧ ¬q ∧ ¬a ∧ o ∨
p ∧ ¬q ∧ ¬a ∧ ¬o ∨
¬p ∧ ¬q ∧ a ∧ o
To remove transitions leading to them, we modify the transition relation to
(q ∧ ¬a ∧ o ∧ next(p) ∨ ¬p ∧ q ∧ next(p) ∧ ¬next(q))
∧
¬(next(p) ∧ ¬next(o) ∨ ¬next(q) ∨ next(p) ∧ next(a))
Left are now just the following transitions (I don't show the other 14 states without transitions):
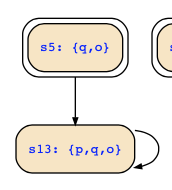
I guess the solution should just consider this clean-up of the structure, i.e., the structure reduced to states on infinite paths. From here, it should be simple to get the final answers.