Given a FSM: A={2Vin,2Vout,I,2Vstate,R}A={2Vin,2Vout,I,2Vstate,R}
where Vin={a}Vin={a}, Vout={o}Vout={o}, Vstate={p,q}Vstate={p,q}, I=I=q,
R=R=(next(q)|q|p)&!(o->a)&next(p)
a)
- label 0:; 1:p; 2:q; 3:p,q;
i.e., node s0-s3 represent states !p&!q, p&!q, !p&q and p&q, respectively. - inputs {a},{};
i.e., two inputs represent a and !a, respectively. - outputs {o},{};
i.e., two outputs represent o and !o, respectively.
After computing the DNF of midterms of transition relation, I got the following representation:
p ^ q ^ o ^ !a ^ !next(q) ^ next(p) v
p ^ q ^ o ^ !a ^ next(q) ^ next(p) v
p ^ !q ^ o ^ !a ^ !next(q) ^ next(p) v
p ^ !q ^ o ^ !a ^ next(q) ^ next(p) v
!p ^ q ^ o ^ !a ^ !next(q) ^ next(p) v
!p ^ q ^ o ^ !a ^ next(q) ^ next(p)
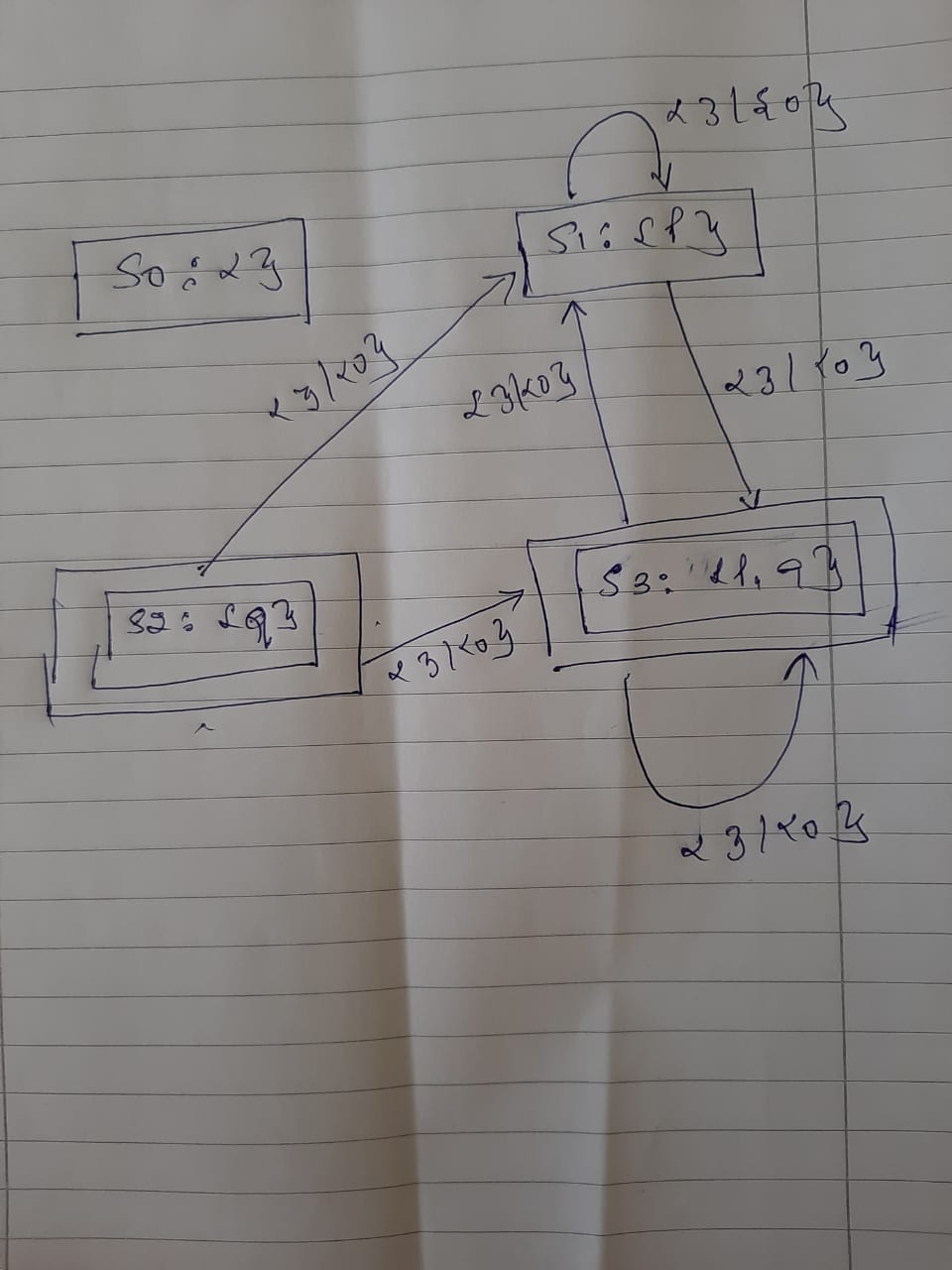
Therefore, I get this transition:
{p,q} ---- 0&!a --- {p}
{p,q} ---- 0&!a --- {p,q}
{p} ---- 0&!a --- {p}
{p} ---- 0&!a --- {p,q}
{q} ---- 0&!a --- {p}
{q} ---- 0&!a --- {p,q}
I got the below diagram:
Below is my answer:
init 2,3;
transitions (1,{},{o},1); (1,{},{o},3); (2,{},{o},1); (2,{},{o},3); (3,{},{o},1); (3,{},{o},3);
It says answer is wrong in the tool.
Not sure which part I have done wrong. can anyone help me on this?