
Use the same label, inputs, and outputs to compute the state transition diagram of the given FSM.
Submit the initial states and transitions in an explicit form:
init 0,1;
transitions (0,{a},{o},1); (0,{},{o},2); (1,{a},{},3); (3,{},{},3);
I converted given FSM to following diagram:
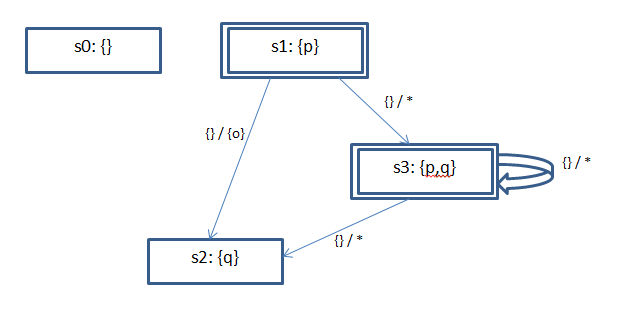
also I interpret R as below:
- there are 2 state variable p,q then we have 4 states
- !(p->a) is p&!a
- next(q)
in this step we have:
p -- !a --> q
p -- !a --> q
p -- !a --> q
p -- !a --> q
- (next(p)|o|q) => because of OR operator we add operand in each state as below, but not sure how is the last one?
p -- !a --> p,q => added next(p)
p -- !a,o --> q => added output o
p,q -- !a --> q => added q
p,q -- !a --> p,q => ???
and below is my answer:
init 1,3;
transitions (1,{},{o},2); (1,{},*,3); (3,{},*,2); (3,{},*,3);
BUT, still when I want to submit it says it is wrong.
May someone assist to elaborate which part I have done wrongly?