Transition relation to state diagram draw

Question

 Sir when I try to draw the diagram from the transition relation. I come up with this truth table. But I cannot draw the diagram. Like on !p&!q I found is !(b|a) | !(b|next(p)). How to draw the transition.? If possible can you please explain the steps. How to draw with the diagram.

Answer 1

To get the transitions which are encoded by a symbolic transition relation like (p <-> b|a&next(p)) & (q<->p&next(q)), we have to list all satisfying assignments of that propositional logic formula. As usual, that can be done in many ways, e.g., using Shannon composition, computing a DNF or a BDD, using the sequent calculus, or some other method.

My recommendation is to make a Shannon decomposition on the current state variables. For the mentioned example, we get

    (p <-> b|a&next(p)) & (q<->p&next(q))
        = (p ? (b|a&next(p)) & (q<->next(q)) 
             : !(b|a&next(p)) & !q )
        = (p ? (q ? (b|a&next(p)) &  next(q) 
                  : (b|a&next(p)) & !next(q)  )
             : (q ? 0
                  : !(b|a&next(p)) ))

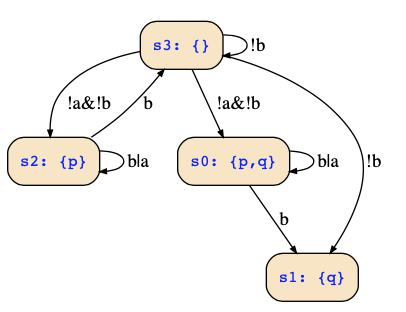
So, we see that from state {q}, there are no outgoing transitions, and all transitions from state {p} are encoded by !(b|a&next(p)), i.e., !b&!a | !b&!next(p)). To get all the transitions, we take the transition relations of the particular states, and further decompose by variables a and b:

    (p ? (q ? (b ?  next(q) : a & next(p) &  next(q) )
            : (b ? !next(q) : a & next(p) & !next(q) ) )
       : (q ? false
            : !b&(!a|!next(p)) ))

Now consider the state {p=0;q=0}, where we get the transitions !b&(!a|!next(p)), or the equivalent form !(b|a) | !(b|next(p)) you got. The satisfying assignments are seen by converting this to a DNF which is !b&!a | !b&!next(p). Hence, with input !b&!a, any state can be reached, and with input !b (and arbitrary a), we can reach the states where p is false, i.e., {} and {q}.

In total, you should get the following transitions: