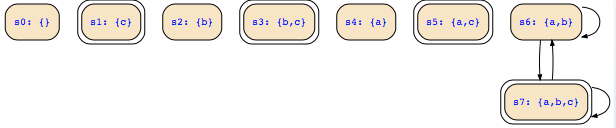
The given transition relation is (a∧b∧a′∧b′) ∨ ¬(a∧b)∧¬(a′∧b′)∧(c↔c′)∧(a⊕a′)∧(b′⊕b′). Since b′⊕b′ is equivalent to false, the entire second disjunct becomes also false, so that the transition relation is equivalent to (a∧b∧a′∧b′). Now the states of the Kripke structure consist of the variable assignments for {a,b,c}, i.e., eight states where we only have transitions from {a,b} and {a,b,c} to these states themselves, i.e.: