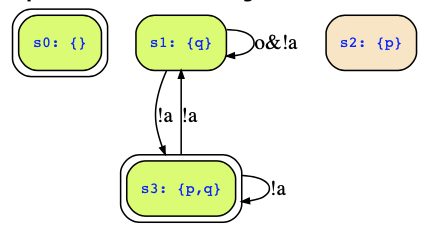
The FSM may have four states {},{p},{q},{p,q} where {},{p,q} are the initial states. The transitions are the satisfying assignments of the transition relation R. Thus, we need to determine those. Looking at R, we can clearly see that next(q) must be true, and !(q->a) means q&!a so that q,a, and next(q) are already determined. Hence, there are no outgoing transitions from {} and neither from {p}. So, consider the remaining states {q},{p,q} which have the following transitions:
- {q} --!a --> {p,q}
- {q} --!a& o --> {q}
- {p,q} --!a --> {q}
- {p,q} --!a --> {p,q}
The FSM looks therefore as follows:
The Kripke structure has states that correspond with the above transitions. To list them, we first have to expand the don't care values of the output for the FSM:
- {q} --!a&!o --> {p,q}
- {q} --!a& o --> {p,q}
- {q} --!a& o --> {q}
- {p,q} --!a&!o --> {q}
- {p,q} --!a& o --> {q}
- {p,q} --!a&!o --> {p,q}
- {p,q} --!a& o --> {p,q}
The above are still the transitions of the FSM, just written without don't care values for the output.
This leads to the following transitions of the Kripke structure where IO can be an arbitrary assignment to the input/output variables a and o (hence the seven transitions listed below lead to 28 transitions of the Kripke structure):
- {q} ----> {p,q}∪IO
- {q,o} ----> {p,q}∪IO
- {q,o} ----> {q}∪IO
- {p,q} ----> {q}∪IO
- {p,q,o} ----> {q}∪IO
- {p,q} ----> {p,q}∪IO
- {p,q,o} ----> {p,q}∪IO