FSM to Kripke
Let's start with the FSM → Kripke transformation. That's slide 8 in the Transition System chapter.
State variables: Each of the new Kripke states represents an FSM state, an input and an output. Simplified speaking, the FSM states variable, FSM input variables and FSM output variables together become the new Kripke state variables.
Transitions: A Kripke states inherits those transitions of the corresponding FSM state that have the input and output variables of the new Kripke state. It is important that the transitions get copied multiple times as we don't know anything about the input and output variables of the successor state.
Example: FSM state {q} has a transition with input a, output o to {p}.
Then the state {q,a,o} gets four transitions going to the four states {p}, {p,a}, {p,o}, {p,a,o}.
Now we only need to talk about the initial states. The initial states of the Kripke structure are those states that correspond to initial states of the FSM. There are two things to take care of:
- Each initial FSM is represented by multiple initial states of the Kripke structure (with different values for input and output)
- We remove initial states of the Kripke structure that have no outgoing transitions (deadends)
Symbolic FSM to FSM diagram
The symbolic representation is discussed on slide 54. The symbolic representation consists of two formulas. One described the transitions and one the initial states. Each state in the diagram represents one valuation of the state variables. So if your states variables are p and q, you get the states {}, {p}, {q}, {p,q}. In the transition formula, we also have input variables (in your example a), and output variables (in your example o). Then we also have the variables for the successor (vulgo: right side) states. In your example, they are p', q' (or as the online tool would say: next(p), next(q)).
Let's look at your example:
R = !(next(p)&next(q)->(a|o)&(q|p)) = …
For better readability, we replace the negated implication and apply De Morgan:
… = next(p)&next(q) & !((a|o)&(q|p)) = next(p)&next(q) & ( !(a|o) | !(q|p) ) = next(p)&next(q) & ( (!a & !o) | (!q & !p) ) = …
Now we multiply out
= (next(p) & next(q) & !a & !o) | (next(p)&next(q) & !q & !p)
Let's look at for example at the valuation with p, q, next(p), next(q) true and a, o false. We don't satisfy the right co-clause but we do satisfy the left co-clause. Great! So we know that there is a self-loop at {p,q} reading !a and outputting !o. Great!
We can continue reading the transition relation like that. All transitions lead to the state {p,q}. All of the four states have this transition to {p,q} reading !a and outputting !o. From the state {} to {p,q} there are four transition, one for each possible valuation of a and o.
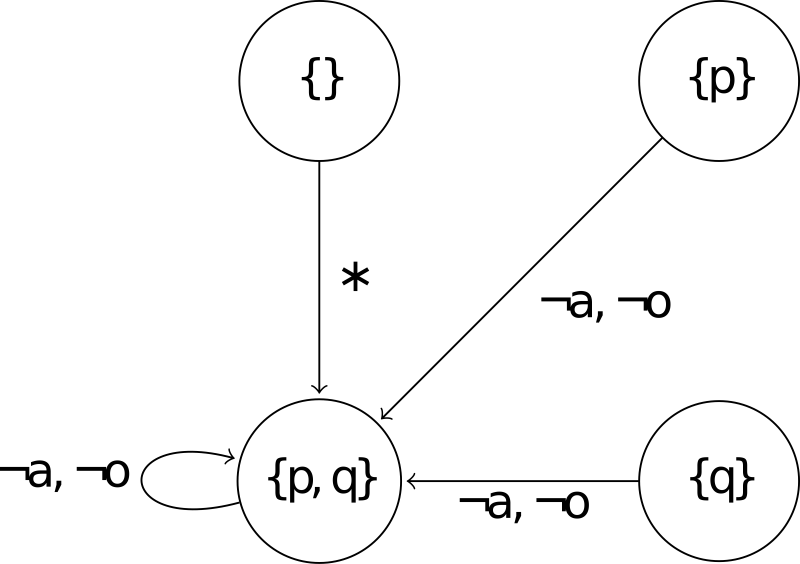
If we now knew the formula for the initial states, we could mark all states that correspond to a satisfying assignment as initial states.
Source Code:
\documentclass[10pt,a4paper]{article}
\usepackage[utf8]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{tikz}
\usetikzlibrary{arrows,automata,positioning}
\begin{document}
\begin{tikzpicture}[shorten >=1pt,node distance=3cm,auto]
\tikzstyle{state}=[minimum size=1.2 cm,draw,shape=circle]
\node[state] (nix){$\{\}$};
\node[state, right of=nix] (p){$\{p\}$};
\node[state,below of=nix] (pq){$\{p,q\}$};
\node[state,right of=pq] (q){$\{q\}$};
\path[->]
(p) edge node {$\neg a, \neg o$} (pq)
(nix) edge node {$\ast$} (pq)
(pq) edge [loop left] node {$\neg a, \neg o$} (pq)
(q) edge node {$\neg a, \neg o$} (pq)
;
\end{tikzpicture}
\end{document}