Given a FSM: A={2Vin,2Vout,I,2Vstate,R}A={2Vin,2Vout,I,2Vstate,R}
where Vin={a}Vin={a}, Vout={o}Vout={o}, Vstate={p,q}Vstate={p,q}, I=I=!p,
R=R=next(q)&(next(p)|(p->q))&!(o|a)
a)
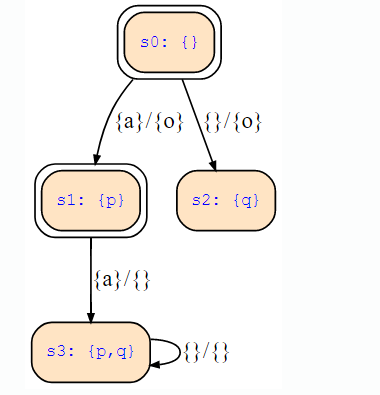
- label 0:; 1:p; 2:q; 3:p,q;
i.e., node s0-s3 represent states !p&!q, p&!q, !p&q and p&q, respectively. - inputs {a},{};
i.e., two inputs represent a and !a, respectively. - outputs {o},{};
i.e., two outputs represent o and !o, respectively. - init 0,1;
i.e., s0 and s1 are initial states. - transitions (0,{a},{o},1); (0,{},{o},2); (1,{a},{},3); (3,{},{},3);
- represents the following state transition diagram in an explicit form:
What is the process to solve this?