Consider the FSM: A={2Vin,2Vout,I,2Vstate,R}A={2Vin,2Vout,I,2Vstate,R}
where Vin={a}Vin={a}, Vout={}Vout={}, Vstate={p,q}Vstate={p,q}, φI=φI=q,
φR=φR=a&p&!q&!next(p)&next(q)|p&q&next(p)&next(q)|p&!a&!q&next(p)&next(q),
and the following state transition diagram:
s0: {}s1: {p}s2: {q}{a}/{}s3: {p,q}{}/{}{}/{}{a}/{}
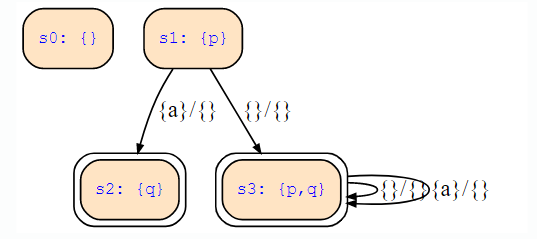
construct the state transition diagram for the corresponding Kripke structure of the given FSM, and solve the following tasks.
Above is the question that I have got.
After solving the above problem;
I get below Kripke structure after removing deadends and unreachable states -
vars a,p,q;
init 0,1;
lablels 0:p,q; 1:p,q,a;
transitions 0->0; 0->1; 1->0; 1->1;
And I get deadend as - {}, {q}, {a}, {q,a}
What's wrong in it?