FSMs to Kripke Structures Q3 [closed]

Question

Consider the FSM: A={2Vin,2Vout,I,2Vstate,R}A={2Vin,2Vout,I,2Vstate,R}
where Vin={a}Vin={a}, Vout={}Vout={}, Vstate={p,q}Vstate={p,q}, φI=φI=q,
φR=φR=a&p&!q&!next(p)&next(q)|p&q&next(p)&next(q)|p&!a&!q&next(p)&next(q),
and the following state transition diagram:
s0: {}s1: {p}s2: {q}{a}/{}s3: {p,q}{}/{}{}/{}{a}/{}

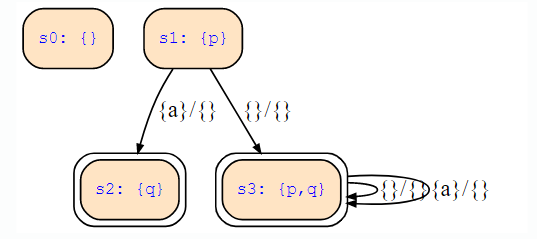
construct the state transition diagram for the corresponding Kripke structure of the given FSM, and solve the following tasks.

Above is the question that I have got.

After solving the above problem;

I get below Kripke structure after removing deadends and unreachable states -

vars a,p,q;

init 0,1;

lablels 0:p,q; 1:p,q,a;

transitions 0->0; 0->1; 1->0; 1->1;

And I get deadend as - {}, {q}, {a}, {q,a}

What's wrong in it?

Answer 1

With your remark I see the problem and edited this answer. Let's have a look at the following FSM where the reachable states are given in green color:

We construct the following Kripke structure for this FSM:

Now, you can clearly see that:

• deadend states are s0,s1,s4,s5
• states with only finite outgoing paths are s0,s1,s4,s5,s6
• initial states are s1,s3,s5,s7
• initial states with at least one outgoing infinite path are s3,s7 
• reachable states are s1,s3,s5,s7
• reachable states with at least one outgoing infinite path are s3,s7 

There is a trouble with this kind of exercise that I try to clarify for years. Some exercises use "deadend state" as "state with only finite outgoing paths", so try that as an alternative solution. I guess that is your trouble here, and I would rather agree with your solution.

Comments

Thanks, but thats not how I'm asked to submit answer. I have to construct a Kripke structure out of the corresponding state diagram. My Kripke structure has 8 states - {}, {a}, {p}, {q}, {pq}, {pa}, {qa}, {pqa},

After solving this, I got

intial states = {pq}, {pqa}
deadends as {}, {a}, {q}, {qa}.

But I'm getting the answer for deadends incorrect.

---

Brill, this works! Thank you! But do we also have to memorize these for exams?

---

In the exams, we will make sure that we are precisely using the definitions!

---

Can I ask how? I have same problem and it is still checked as wrong :(

---

I checked your submission and you entered something like s0 ∨ s1∨ ... . However, you have to submit a formula using the variables of the Kripke structure, i.e., a,p,q.