From transition relation to transition diagram

Question

I have tried making Shannon normal form, because of 2 eqivalence and 2 xor operation its becoming too long. 

I tried the truth table it is too long too.

I tried setting truth table between q2' and q1', still so many conditions, is there any way to read the formula in the short cut because it is just for 2 marks in exam paper but its getting too long to solve.

Answer 1

The problem with the SAT problem is that there is no method that is the best. Sometimes, it is okay to just make a truth table, sometimes a BDD is fine, and sometimes just converting to some other normal form will do. 

In your example, I suggest the following partial evaluation approach: Make case distinctions for q1 and q2 since that will eliminate these variables and will reduce a lot of the remaining formula. This will give you all transitions that will start in one of the four possible states. 

Let's do that with your transition relation

            (next(q2) <-> (a xor q1) | (a & q2)) & 
            (next(q1) <-> (a xor q2) | (a & q1))

  q1=0 & q2=0:

        (next(q2) <-> (a xor q1) | (a & q2)) & 
        (next(q1) <-> (a xor q2) | (a & q1))
        =
        (next(q2) <-> a) & 
        (next(q1) <-> a)

        which gives you now the transitions

            {q1=0;q2=0} --!a--> {q1=0;q2=0}
            {q1=0;q2=0} -- a--> {q1=1;q2=1}



   q1=0 & q2=1:

        (next(q2) <-> (a xor q1) | (a & q2)) & 
        (next(q1) <-> (a xor q2) | (a & q1))
        =
        (next(q2) <-> a | a) & 
        (next(q1) <-> !a)
        =
        (next(q2) <->  a) & 
        (next(q1) <-> !a)

        which gives you now the transitions
        
            {q1=0;q2=1} --!a--> {q1=1;q2=0}
            {q1=0;q2=1} -- a--> {q1=0;q2=1}


   q1=1 & q2=0:

        (next(q2) <-> (a xor q1) | (a & q2)) & 
        (next(q1) <-> (a xor q2) | (a & q1))
        =
        (next(q2) <-> !a) & 
        (next(q1) <-> a | a)
        =
        (next(q2) <-> !a) & 
        (next(q1) <-> a)

        which gives you now the transitions

            {q1=1;q2=0} --!a--> {q1=0;q2=1}
            {q1=1;q2=0} -- a--> {q1=1;q2=0}


   q1=1 & q2=1:

        (next(q2) <-> (a xor q1) | (a & q2)) & 
        (next(q1) <-> (a xor q2) | (a & q1))
        =
        (next(q2) <-> !a | a) & 
        (next(q1) <-> !a | a)
        =
        (next(q2) <-> true) & 
        (next(q1) <-> true)

        which gives you now the transitions

            {q1=1;q2=1} --!a--> {q1=1;q2=1}
            {q1=1;q2=1} -- a--> {q1=1;q2=1}

and that is the following state transition system:

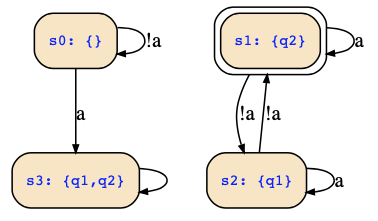
If just the reachable states would have been of interest, it would have been good to first state with the initial state s1, and then to continue with the next state s2 so that we would not have had to consider s0 and s3 at all. 

Comments

Thank you. I understood now.