Here is how I solve it: You rewrite the formula such that any occurrence of next(p) is written as pX (or any other new kind of name that you can associate with the original name p). In your case, the formula becomes
aX&a&(b|b<->cX)
Then, you need to find the satisfying assignments. Truth tables are usually too big, so better use BDDs and/or the generation of a DNF from the BDD. In your case, I get
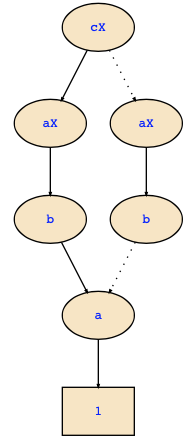
which has the following DNF:
a&b&aX&cX|a&!b&aX&!cX
Hence, you have the following transitions:
{a,b,*} -> {a,*,c}
{a,!b,*} -> {a,*,!c}
where * means a don't care, thus,
{a,b} -> {a,c}
{a,b} -> {a,b,c}
{a,b,c} -> {a,c}
{a,b,c} -> {a,b,c}
{a} -> {a}
{a} -> {a,b}
{a,c} -> {a}
{a,c} -> {a,b}