Indeed, that is not so easy to see, but the equation "length of kernel = initiation interval π" is indeed true. To clarify, consider the examples below first, and then the general case.
As you know, the initiation interval π is the time gap between starting the different loop bodies that then overlap in execution. For instance, considering a general loop statement
for(i=1..n-1) {
I1[i];
:
Im[i];
}
with an initiation intervall π=1, we would get
I1[1];
I2[1]; I1[2];
I3[1]; I2[2]; I1[3];
I4[1]; I3[2]; I2[3]; I1[4];
:
and therefore the following kernel of length π=1:
I4[i]; I3[i+1]; I2[i+2]; I1[i+3];
Next, consider π=2:
I1[1];
I2[1];
I3[1]; I1[2];
I4[1]; I2[2];
I5[1]; I3[2]; I1[3];
I6[1]; I4[2]; I2[3];
I7[1]; I5[2]; I3[3]; I1[4];
I8[1]; I6[2]; I4[3]; I2[4];
What is the kernel here? It has length π=2 and is as follows:
I7[i]; I5[i+1]; I3[i+2]; I1[i+3];
I8[i]; I6[i+1]; I4[i+2]; I2[i+3];
You can generalize this and in the general case, where we may consider a loop body with m=p*π many statements S[i][0];...;S[i][p*π -1], you would schedule the statements S[i][j] as follows
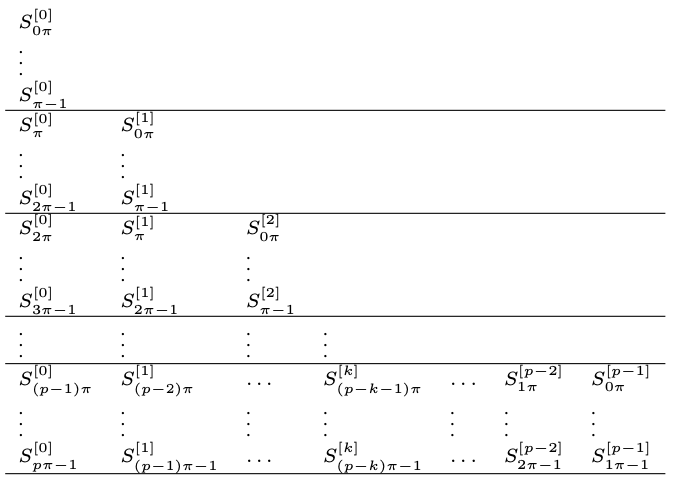
and thus you get the following kernel:

which has π rows and p columns. The length of the kernel is now the number of rows of the above block, i.e., π, and in each each row, we can execute p of the statements in parallel.
Bytheway, you can now also see the pipeline: in the above case, the entire execution of a loop body S[i][0];...;S[i][p*π -1] is split into p stages where stage k executes S[i][k*π];...;S[i][k*π -1]. The execution of one stage of a loop body overlaps with the stages of p-1 other loop bodies.