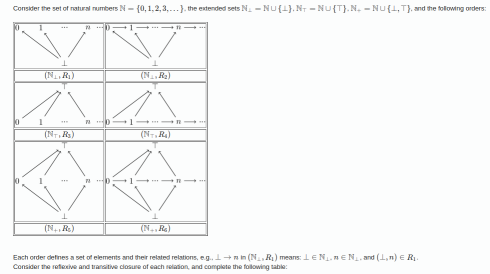
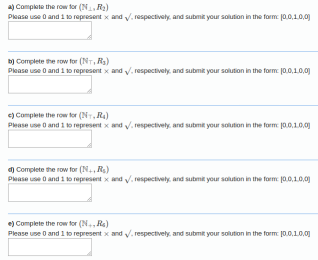
for R2 I think:
-it is total order because all the elements can be compared and
totality: ∀x, y ∈ D. x ⊑ y ∨ y ⊑ x is valid.
-it's directed set because all the elements have upper and lower bound
-it is partial order because it satisfies reflexivity, antisymmetry and transitivity.
-it's lattice becasue all elements have sup and inf
-it's lattice complete because all elements have sup and inf
but my solution is not correct. would you please help me?
plus I don't know the meaning of these signs: {⊥,⊤} , N+