To clarify: initial states are states that satisfy the initial condition; deadend states are states without outgoing transitions; reachable states are states that have a path from an initial state.
The exercise was asking in a) to remove initial states that are also deadend states from the set of initial states. That is a new structure that shall be considered in part b) where you should find on that structure the reachable states. Obviously now the former initial states with deadends are gone. In part c) you then remove the deadends, and in part d) also the unreachable states.
In your case, we consider a Kripke structure with variables p,q,a, initial states !p&!q and the following transition relation R:
a & !p & q & !next(p) & !next(q) |
a & !p & !q & next(p) & !next(q) |
a & p & !q & next(p) & next(q) |
a & p & q & next(p) & next(q)
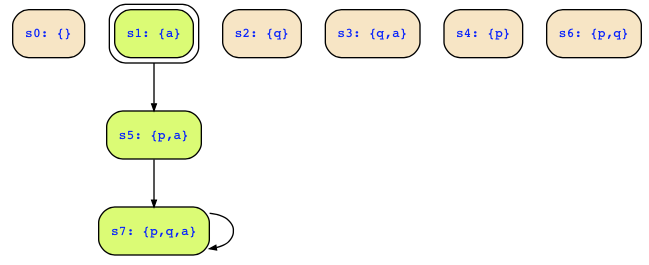
The Kripke structure looks as follows:
Looking at the Kripke structure, you can see
- initial states s0,s1 described by !a&!p&!q|a&!p&!q
- deadend states s0,s2,s4,s6 described by !a
- unreachble states s2,s3 described by !a&!p&q|a&!p&q
We now want to clean up the Kripke structure in that we remove transitions to deadend states and transitions from unreachable states.
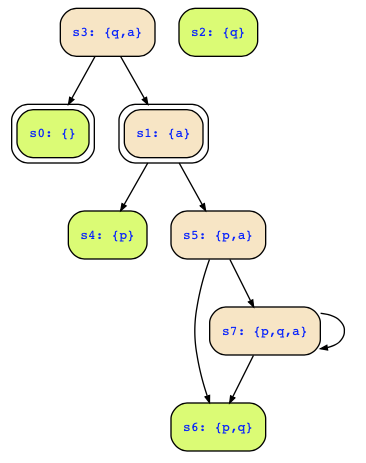
a) Initial states without deadend states are only s1, i.e., a&!p&!q. That changes our Kripke structure as follows:
b) For the above Kripke structure, we ask now for the reachable states which are now states s1,s4,s5,s6,s7 where states s4,s6 have however only finite paths (they are however still reachable). Reachable states are therefore a&!p&!q | !a&p&!q | a&p&!q | !a&p&q | a&p&q.
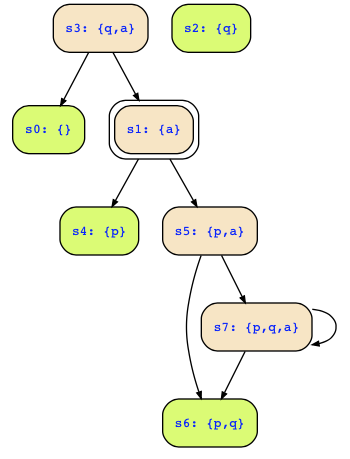
c) Removing transitions to deadend states is done by using the following transition relation
(
a & !p & q & !next(p) & !next(q) |
a & !p & !q & next(p) & !next(q) |
a & p & !q & next(p) & next(q) |
a & p & q & next(p) & next(q)
)
& next(a)
which looks as follows
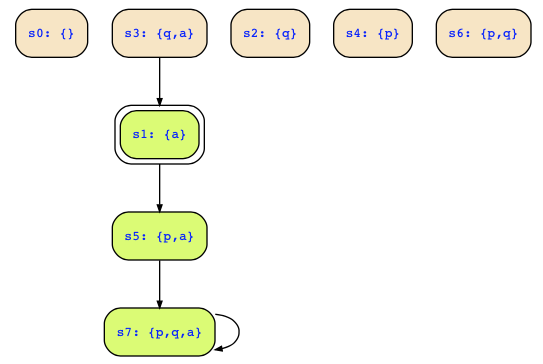
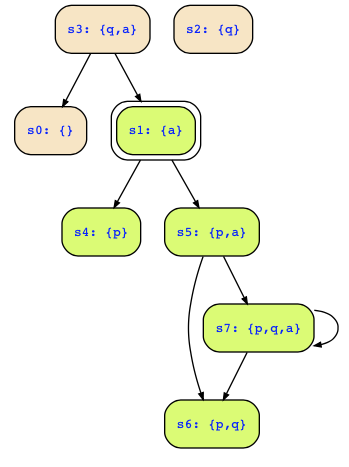
d) In the above structure, only states s1,s5,s7 are reachable. Thus, we just have to remove the transition from state s3 to remove transitions among unreachable states:
(
a & !p & q & !next(p) & !next(q) |
a & !p & !q & next(p) & !next(q) |
a & p & !q & next(p) & next(q) |
a & p & q & next(p) & next(q)
)
& next(a)
& !(a&!p&q)This is finally the following structure: