We consider a Kripke structure with variables p,q,a, initial states !p&!q and the following transition relation R:
a & !p & q & !next(p) & !next(q) |
a & !p & !q & next(p) & !next(q) |
a & p & !q & next(p) & next(q) |
a & p & q & next(p) & next(q)
The Kripke structure looks as follows:
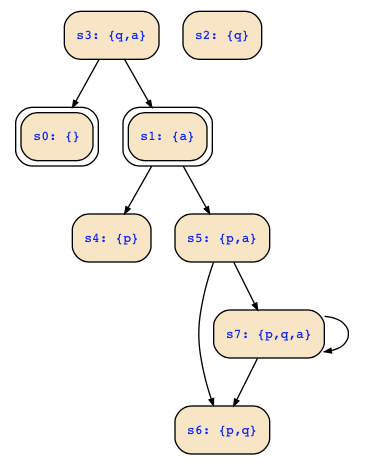
Looking at the Kripke structure, you can see
- initial states s0,s4 described by !a&!p&!q|!a&!p&q
- deadend states s0,s1,s2,s3 described by !a
- unreachble states s1,s5 described by !a&!p&q|a&!p&q
We now want to clean up the Kripke structure in that we remove transitions to deadend states and transitions from unreachable states.
a) Initial states without deadend states are only s4, i.e., a&!p&!q
b) As Martin said, we should consider in this part states that are reachable from the new initial states, but do not yet make changes to the transition relation.
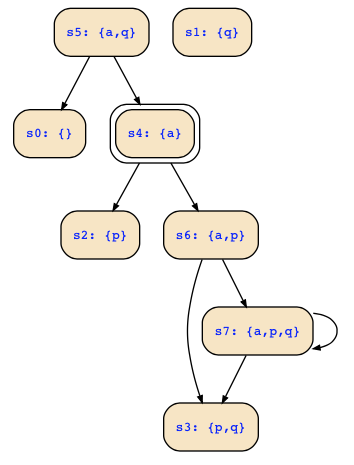
I would say from s4 (the only initial state), states s2,s3,s4,s6,s7 are reachable.
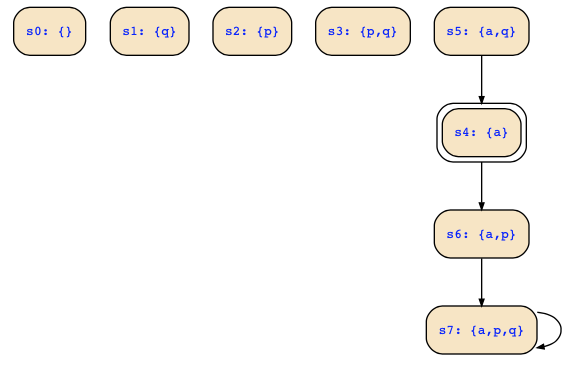
c) Removing transitions to deadend states is done by using the following transition relation
(
a & !p & q & !next(p) & !next(q) |
a & !p & !q & next(p) & !next(q) |
a & p & !q & next(p) & next(q) |
a & p & q & next(p) & next(q)
)
& next(a)
which looks as follows
d) Removing transitions among unreachable states yields the following transition relation and Kripke structure
(
a & !p & q & !next(p) & !next(q) |
a & !p & !q & next(p) & !next(q) |
a & p & !q & next(p) & next(q) |
a & p & q & next(p) & next(q)
)
& next(a)
& !(!a&!p&q|a&!p&q)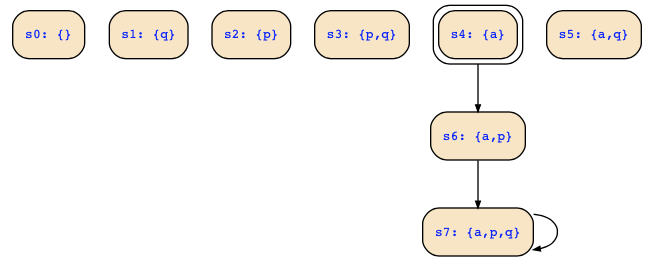
This is the Kripke structure you have constructed, and probably you have also use it already to solve part b), but that was maybe too early. Am I right?