We are talking about this state transition system:
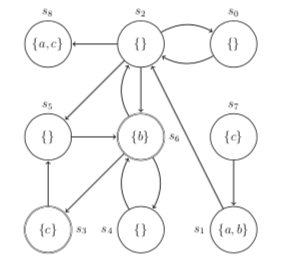
States s3,s7,s8 are states labeled with c. Thus, all infinite paths leaving these states satisfy [b WU c] and even the strong until [b SU c] (even if b would be false) since c is initially true on these paths. Now, s8 does not have infinite outgoing paths while s3 and s7 have these. This does however not matter for A quantifiers, since their meaning is: "If there are infinite outgoing paths, then all of them have to satisfy the path property. If there is no infinite outgoing path, then ALL formulas AΦ are true in that state."
Hence, any formula AΦ would hold in state s8 (so it is not needed that c was on the label). Saying "any" is really meant this way, since even A false holds in state s8 (as in any other state without outgoing infinite path).