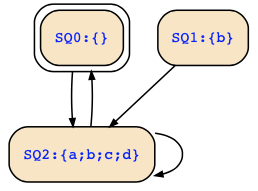
You did not tell us the set of variables which are known by the given structures. If I assume that both are given over the same set of variables {a,b,c,d} then your product structure is wrong since only the states S0 and Q1 would have compatible labels. The product structure would therefore just consist of their combined product state without any transitions.
If I assume that K1 has variables {b,c,d} and K2 has variables {a,c,d}, then the result would be the following which is again different to yours:
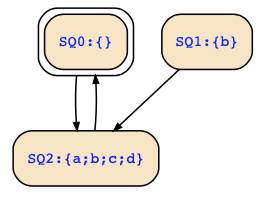
Note that SQ1 is not reachable.
Taking into account the comment of ftego below, I missed a transition. Putting things together, we have the following two structures over {b,c,d} and {a,c,d}, respectively,
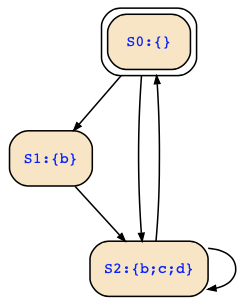
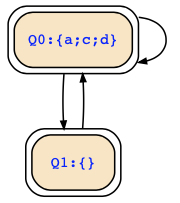
and their product is then: