Thank you for your question! I'm really glad to see that this exercise is already being worked on!
It looks to me that you are entering the solution for x ↔ (y1 ∧ y2) or x <-> (y1 & y2). Please note that the circonflexe ^ is XOR or ⊕.
Out of curiosity: Which online tools did you use to verify your solution and how did you do so? I used the Embedded Systems Group's teaching tools on propositional logic. As an output, I used the truth table, and as an input used entered the variables x,y1,y2 and the formulas
(¬x ∨ y1) ∧ (¬x ∨ y2) ∧ (¬y1 ∨ ¬y2 ∨ x);
x <-> (y1 ^ y2)
The result was this truth table:
| x | y1 | y2 | (!x|y1)&(!x|y2)&(!y1|!y2|x) | x<->!(y1<->y2) |
|---|
| 0 | 0 | 0 | 1 | 1 |
|---|
| 0 | 0 | 1 | 1 | 0 |
|---|
| 0 | 1 | 0 | 1 | 0 |
|---|
| 0 | 1 | 1 | 0 | 1 |
|---|
| 1 | 0 | 0 | 0 | 0 |
|---|
| 1 | 0 | 1 | 0 | 1 |
|---|
| 1 | 1 | 0 | 0 | 1 |
|---|
| 1 | 1 | 1 | 1 | 0 |
|---|
You can see that only for two assignments the formulas evaluate to the same result. Another way of telling these formulas apart would have been connecting the two formulas with ↔ and checking it for tautology. The following sequent calculus proof tree is generated for an XOR between the two formulas. (Note that XOR is precisely the negation of ↔.)
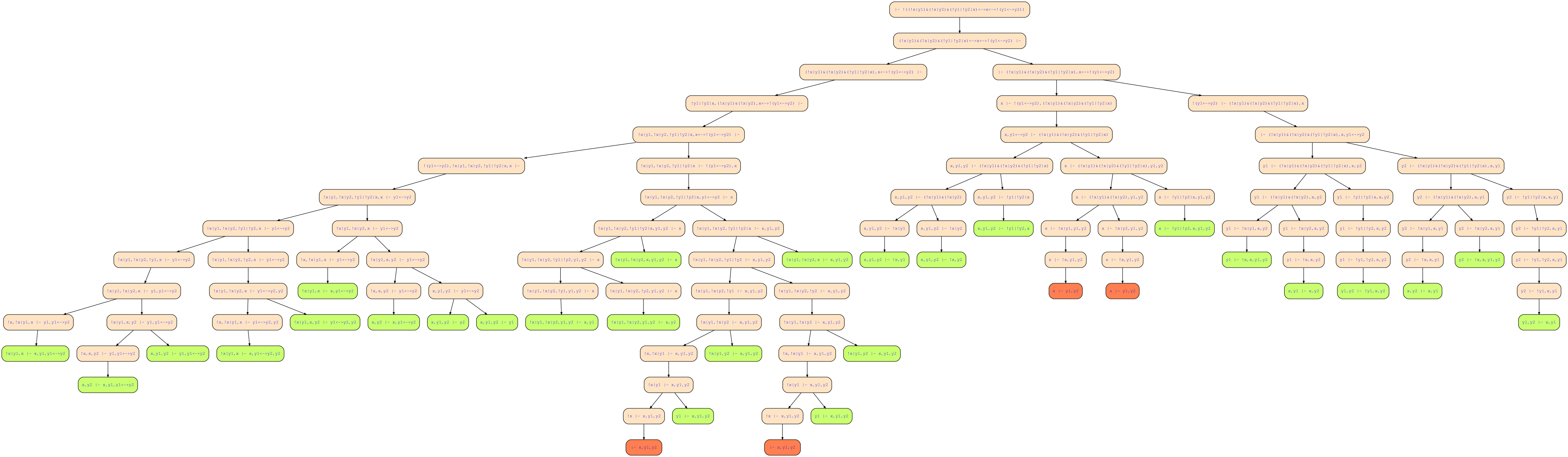
From the green leaves, you can tell that the new xor-formula is satisfiable which means that its operands differ.
Here is another trick on reading the resulting cnf: A → B is the same as (¬A ∨ B), hence your formula can be read as
(X → Y1) ∧ (X → Y2) ∧ (¬X → (¬Y1 ∨ ¬Y2))
This means that there three if-statements:
- if Y is satisfied, Y1 is satisfied too
- if Y is satisfied, Y2 is satisfied too
- if Y is not satisfied, at least one of Y1, Y2 is not satisfied
One can easily tell that this this the conjunction ∧.