Schauen Sie sich dazu die Folie 181 für einen LR(0) Parser an. Dort sehen Sie folgendes
- Shift-Aktion: Wenn ein Zustand qi eine Regel A->α.aβ mit einem Terminalzeichen a enthält, dann führt der Parser eine Shift-Aktion aus und geht in den Folgezustand gemäß dem Automaten über.
- Accept-Aktion: Wenn ein Zustand qi die Regel S′ → S. enthält und die Eingabe leer ist, wird die Eingabe akzeptiert.
- Reduce-Aktion: Wenn qi eine "vollständige Regel" B → γ. enhält, dann führt der Parser eine Reduktion mit der Regel B → γ aus. Dazu wird vom Stack das Wort γ, welches sich oben auf dem Stack befindet, mit allen darin enthaltenen Zuständen entfernt und vom darunter liegenden Zustand wird dann B gelesen und ein Folgezustand gemäß dem Automaten erreicht.
Die Tabelle wird nun wie oben beschrieben definiert. Leider gibt es einige Grammatiken, die nicht die LR(0)-Eigenschaft haben, die man aber dennoch einfach in Griff bekommt, wenn sie die SLR(1)-Eigenschaft haben. Diese wird auf Folie 184 erklärt und verfeinert die Reduce-Aktionen so, dass zusätzlich verlangt wird, dass der nächste Buchstabe im Eingabwort in Follow(B) liegen muss. Ich denke, dass die Folie 184 die Antwort auf Ihre Frage liefert!
Schauen wir nun den Automaten aus der Klausur 30.03.2021 an:
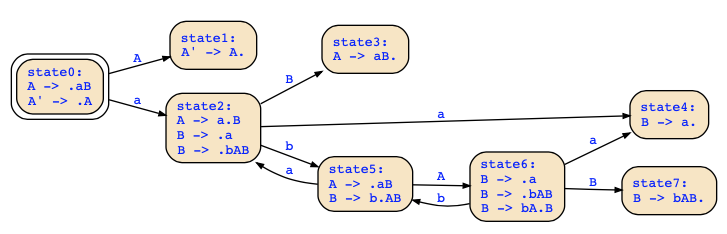
Wir finden folgende vollständige Regeln (also mit Punkt am Ende):
- A' -> A. in state1
- A -> aB. in state3
- B -> a. in state4
- B -> bAB. in state7
Bei einem LR(0)-Parser würden diese Reduce-Aktionen in den jeweiligen Zuständen ausgeführt werden, bei einem SLR(1)-Parser jedoch nur, wenn das nächste Eingabezeichen in Follow(A) bzw. Follow(B) liegt.
Da wir in diesem Beispiel Follow(A) = Follow(B) = {$,a,b} haben, werden diese Reduce-Aktionen also nur für die nächsten Eingaben $,a,b ausgeführt. Da dieser Automat aber ohnehin die LR(0)-Eigenschaft hat, wäre es nicht schlimm, diese Aktionen grundsätzlich (also für alle Eingaben) in diesen Zuständen auszuführen, da sie keine Shift/Reduce-Konflikte provozieren würden.
Schauen wir nun aber die Klausur vom 23.07.2021 an: Hier haben wir folgende Grammatik:
S->Ab|bS
A->aA|a
für die der folgende Automat generiert wird:
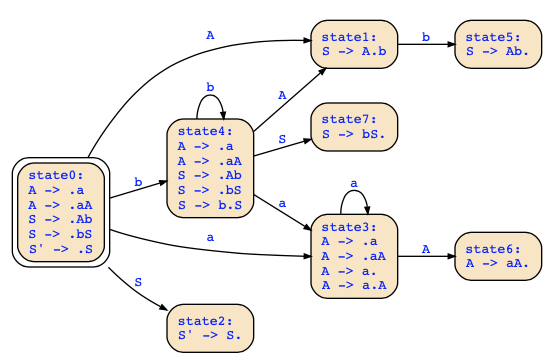
Wir finden folgende vollständige Regeln (also mit Punkt am Ende):
- S' -> S. in state2
- A -> a. in state3
- S -> Ab. in state5
- A -> aA. in state6
- S -> bS. in state7
Diese Grammatik hat nicht die LR(0)-Eigenschaft, da wir im Zustand state3 sowohl mit A -> a. reduzieren könnten als auch "a" schieben könnten.
Aber die Grammatik hat die SLR(1)-Eigenschaft, denn wir haben Follow(S) = {$} und Follow(A) = {b}. Also wird in Zustand state3 nur dann mit A -> a reduziert, wenn die nächste Eingabe b ist, während bei Eingabe a geschoben wird. Entsprechend sind die anderen Aktionen definiert.
Mit SLR(1)-Parsern kann man alle deterministische kontextfreie Sprachen parsen, so dass man in der Regel diese Parser verwendet und nicht die LR(0)-Parser, die fast identisch sind, aber Shift/Reduce-Konflikte haben, die SRL(1)-Parser nicht haben.