The formula in question is a shorthand description of a weak consistency memory model. As you know, we consider for each process a sequence of read/write actions (so we do not analyze source code with control flow). These sequences determine the process order which is a total order when restricting it to the read/write actions of one process, and it is a partial order for all processes since the actions of different processes are not ordered by it. Note that partial/total orders are transitive, so that p1<p2 and p2<p3 implies also p1<p3, so even though p1 and p3 are only in consideration, they are still ordered even though p2 is absent.
For memory consistency, we have to make sure that a read operation is consistent with the current state of the main memory which means we can only schedule read(x,v) if v is the current value of variable x in the main memory.
The definition of Cache Consistency is as follows:
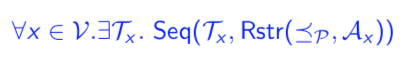
This formula is to be read as follows: For every variable x, there must be a total order T_x that contains the restriction of the process order to the read/write actions on variable x. So, to check whether a given set of processes (i.e., sequences of read/write actions) are cache consistent, we do the following for every variable x: (1) remove all actions not acting on x and (2) schedule the remaining ones (acting on x ) into a memory consistent sequence (which is the total order T_x).
So, the short answer is: The process order has to be considered as well, of course, but only its restriction to the read/write actions on a considered variable x which may be empty. Let's consider a concrete example:
thread P
p1: write(x,1)
p2: read(y,3)
p3: read(x,1)
thread Q
q1: read(x,1)
q2: write(x,2)
q3: write(y,3)
The process order consists of the following pairs:
(p1,p2),(p2,p3),(p1,p3),(q1,q2),(q2,q3),(q1,q3)
Its restriction to actions on variable x is:
(p1,p3),(q1,q2)
and its restriction to actions on variable y is empty! The schedules for variables x and y are therefore as follows and prove that the example is cache consistent
sequentialization for y:
q3: write(y,3)
p2: read(y,3)
sequentialization for x:
p1: write(x,1)
p3: read(x,1)
q1: read(x,1)
q2: write(x,2)