Well, assume your FSM is the following one: input variables Vin={a}, output variables Vout={o}, state variables Vstate={p,q}, initial state condition I is q<->p, and the transition relation R is next(q)&!(q->a)&(next(p)|o|p). There was a recent question that asked how to generate the states and transition of the FSM which looked then as follows:
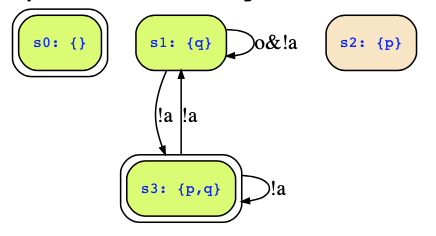
Now, here you agree with me that initial states are s0 and s3 and reachable states are s0,s1,s3. Their symbolic encodings are minterms of the state variables, i.e.,
- s0: ¬p⋀¬q
- s1: ¬p⋀q
- s3 : p⋀q
Sets of states are then simple disjunctions of these states, which leads to formulas in DNF (if not simplified) so that
- the initial states are ¬p⋀¬q ⋁ p⋀q
- and the reachable states are ¬p⋀¬q ⋁ p⋀q ⋁ ¬p⋀q
Of course, you can also directly convert the initial condition q<->p into a DNF, but make sure that this DNF is then a disjunction of minterms over the state variables. The reachable states cannot be computed that easily from the initial states and the transition relation. To that end, we have to compute a fix point on the formulas as done by the µ-calculus formula µx. Init ⋁ <:>x where <:> denotes the existential predecessor states.
Similar arguments apply to the Kripke structure.