I am solving exam problem 16.02.2022 Q 6 a - 2022.02.16.vrs.solutions.pdf (uni-kl.de)

The first part is clear where we translate negation of LTL to the omega automata but for the second part I have some query.
Q1 : I interpreted X q0 , X q1, X q2 as q0', q1', q2' respectively in transition relation because it says in the next time (next state) ? Is it right ?
Q2 : Based on above interpretation I calculated the SNF normally and came as below (solution). But for some combination of q0, q1 and q2 the result is not as written in exam solutions for example for q0 = 0, q1 = 1, q2 = 0. Could you please confirm if my SNF is right or there is mistake in this ?
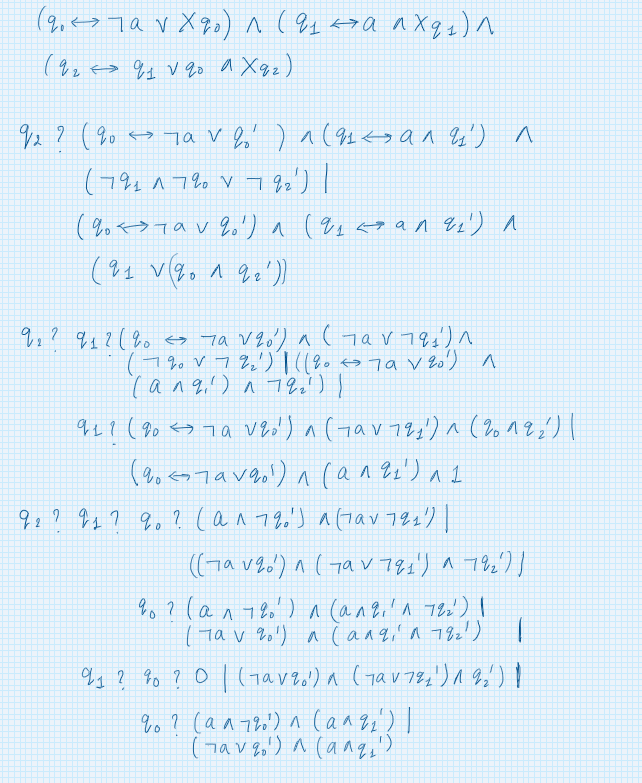
I tried with tool but tool calculates SNF for every variable so it was hard to interpret from there (or you can please guide me how to calculate SNF while not calculating the result for certain variables and give the result in propositional formula)