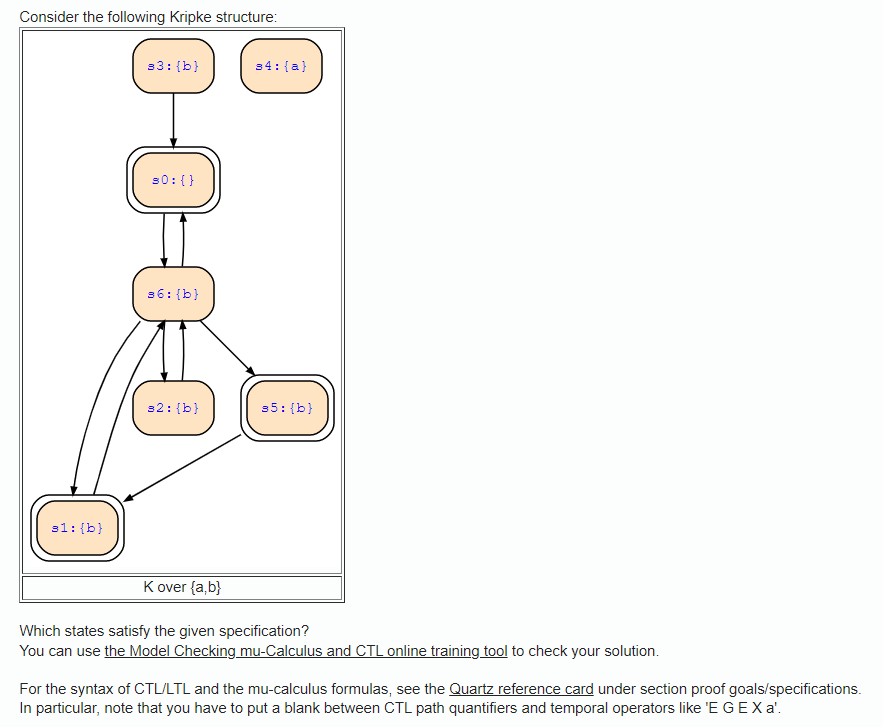
Q c) Compute the set of states satisfy
S2=A G (a&b)
I tried to solve this question as below :
Set of state satisfy a is {s4}
Set of states satisfy b are {s1,s2,s3,s5,s6}
Set of states satisfy the conjunction of a & b is {}
Now, at this point I am confused why A G ({}) is {s4} ?, as there is no path from initial states to s4 and s4 is an unreachable state.