VRS Sheet 5, 1.c and 1.d, obtaining R1 and R2 from R`

Question

R1 is obtained by removing the transitions to deadends so solution is R & ! (deadend)

I have given following solution but it is not accepted.

(a&p&q&next(p)&next(q)|p&!q&next(p)&next(q)|!a&!p&!q&next(p)&next(q)) & !(q&!p&!a | !next(p)&!next(q)&a | !next(p)&next(q)&a |     p&q&!a)

Similarly, in 1.d, R2 is obtained by removing the transitions from/to unreachable states, meaning R1 & !(unreachable states)?

Is there any conceptual error in my solutions? its not accepting the answers.

Answer 1

In the first parentheses you list all of the four possible cases (the middle one includes 2) which is the correct idea. However you forgot to specify whether next(a) or !next(a) should hold, which results in a total of 8 transitions (instead of the four you probably want). Thus you need to add next(a) to all of these cases (as s3 requires the input "a" for every transition starting there). Other than that you don't actually need any of the parts on the right of these parentheses, i.e. you can omit "!(q&!p&!a | !next(p)&!next(q)&a | !next(p)&next(q)&a |     p&q&!a)" as the terms there do not overlap with the ones in the first parentheses and thus do not add additional constraints.

Answer 2

It appears to me that you consider a FSM with state variables p,q and input variable "a" with initial states specified by "p" and the transitions specified by

    a&p&q&next(p)&next(q)|p&!q&next(p)&next(q)|!a&!p&!q&next(p)&next(q)

Using https://es.cs.uni-kl.de/tools/teaching/SymbolicStateTrans.html, we can quickly consider a graphical illustration of that state transition diagram:

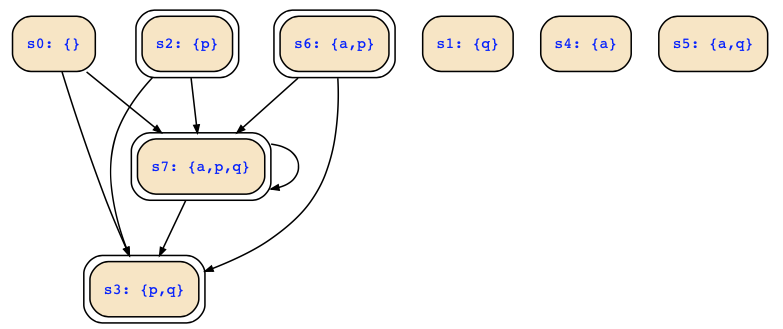
That nice tool also computes the follow sets of states for us:

•     initial states:   {s2,s3,s6,s7}
•     reachable states: {s2,s3,s6,s7}
•     dead(end) states: {s1,s3,s4,s5}
•     finally dead(end) states: {s1,s3,s4,s5}

They can be easily represented as follows (note that p&!q&!a | p&q&!a | p&!q&a | p&q&a is equivalent to p and that !p&q&!a | p&q&!a | !p&!q&a | !p&q&a is equivalent to !p&a | q&!a):

•     initial states:   p 
•     reachable states: p
•     dead(end) states: !p&a | q&!a
•     finally dead(end) states: !p&a | q&!a

After this preparation, let's consider the solution of the exercise:

1a) is not well-posed. The initial states may contain deadend states, and are simply encoded by the formula p as we have seen above. As 1a continues with mentioning that we should compute initial states without deadend states, we should submit p & !(!p&a | q&!a) or some formula equivalent to that one.

1b) we already determined the reachable states as the initial states, so the solution is just p.

1c) Removing the transitions to deadend states is done by R&!next(deadend) and not by R&!deadend as you stated above, i.e., 

(a&p&q&next(p)&next(q)|p&!q&next(p)&next(q)|!a&!p&!q&next(p)&next(q)) &!next(!p&a | q&!a)

However, we must shift the next operator inwards:

    (a&p&q&next(p)&next(q)|p&!q&next(p)&next(q)|!a&!p&!q&next(p)&next(q))
    &!(!next(p)&next(a) | next(q)&!next(a))

which is equivalent to the following four transitions s0->s7, s2->s7, s6->s7, s7->s7:

      p&a&next(p)&next(q)&next(a) |
    !q&!a&next(p)&next(q)&next(a)

1d) Next, we shall remove transitions from/to unreachable states from the transitions in 1c which is done by 

    R1c & !unreachable & !next(unreachable)

The only unreachble state left is state s0 which is encoded by !p&!q&!a, so it should be easy to calculate this, e.g., as 

    (
        p&a&next(p)&next(q)&next(a) |
      !q&!a&next(p)&next(q)&next(a)
    ) & !(!p&!q&!a) & !(!next(p)&!next(q)&!next(a))

which is equivalent to

    p   &a&next(p)&next(q)&next(a)  |  p&!q  &next(p)&next(q)&next(a)

or also equivalent to (which shows the three transitions):

    p&!q&!a&next(p)&next(q)&next(a)  | 
    p&!q& a&next(p)&next(q)&next(a)  | 
    p& q& a&next(p)&next(q)&next(a)