It appears to me that you consider a FSM with state variables p,q and input variable "a" with initial states specified by "p" and the transitions specified by
a&p&q&next(p)&next(q)|p&!q&next(p)&next(q)|!a&!p&!q&next(p)&next(q)
Using https://es.cs.uni-kl.de/tools/teaching/SymbolicStateTrans.html, we can quickly consider a graphical illustration of that state transition diagram:
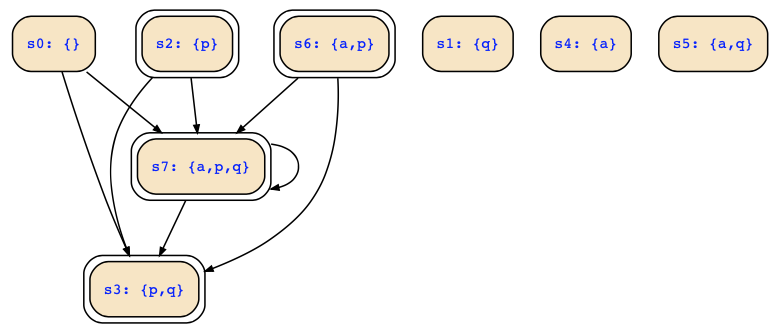
That nice tool also computes the follow sets of states for us:
- initial states: {s2,s3,s6,s7}
- reachable states: {s2,s3,s6,s7}
- dead(end) states: {s1,s3,s4,s5}
- finally dead(end) states: {s1,s3,s4,s5}
They can be easily represented as follows (note that p&!q&!a | p&q&!a | p&!q&a | p&q&a is equivalent to p and that !p&q&!a | p&q&!a | !p&!q&a | !p&q&a is equivalent to !p&a | q&!a):
- initial states: p
- reachable states: p
- dead(end) states: !p&a | q&!a
- finally dead(end) states: !p&a | q&!a
After this preparation, let's consider the solution of the exercise:
1a) is not well-posed. The initial states may contain deadend states, and are simply encoded by the formula p as we have seen above. As 1a continues with mentioning that we should compute initial states without deadend states, we should submit p & !(!p&a | q&!a) or some formula equivalent to that one.
1b) we already determined the reachable states as the initial states, so the solution is just p.
1c) Removing the transitions to deadend states is done by R&!next(deadend) and not by R&!deadend as you stated above, i.e.,
(a&p&q&next(p)&next(q)|p&!q&next(p)&next(q)|!a&!p&!q&next(p)&next(q)) &!next(!p&a | q&!a)
However, we must shift the next operator inwards:
(a&p&q&next(p)&next(q)|p&!q&next(p)&next(q)|!a&!p&!q&next(p)&next(q))
&!(!next(p)&next(a) | next(q)&!next(a))which is equivalent to the following four transitions s0->s7, s2->s7, s6->s7, s7->s7:
p&a&next(p)&next(q)&next(a) |
!q&!a&next(p)&next(q)&next(a)1d) Next, we shall remove transitions from/to unreachable states from the transitions in 1c which is done by
R1c & !unreachable & !next(unreachable)
The only unreachble state left is state s0 which is encoded by !p&!q&!a, so it should be easy to calculate this, e.g., as
(
p&a&next(p)&next(q)&next(a) |
!q&!a&next(p)&next(q)&next(a)
) & !(!p&!q&!a) & !(!next(p)&!next(q)&!next(a))which is equivalent to
p &a&next(p)&next(q)&next(a) | p&!q &next(p)&next(q)&next(a)
or also equivalent to (which shows the three transitions):
p&!q&!a&next(p)&next(q)&next(a) |
p&!q& a&next(p)&next(q)&next(a) |
p& q& a&next(p)&next(q)&next(a)