About the first point: To detail Martin's explanation, let us abbreviate b := EFa (which is what he calls the inner criterion), then we find that state {s0,s1} satisfy EFa. Thus, let's label then these states by b (see structure below), and then check EGb. I think now you will agree that only state s0 satisfies EGb, i.e., EGEFa, right?
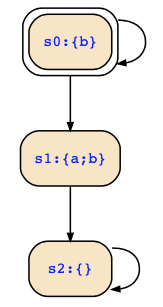
As you say, EG EF means that there is a path such that we always CAN reach a. It does not say that we actually do reach a. Looping in state s0, allows us to always reach a, if we want, even though we never do so.
About the second point: How to identify state/path formulas? That is quite simple, since the following and only the following are state formulas:
- propositional formulas are state formulas, i.e., all formulas without any temporal operator X,G,F,WU,SU,WB,SB,WW,SW or path quantifier E,A
- every formula starting with a path quantifier E or A is a state formula
- state formulas are closed under boolean operators
Hence, to decide whether a given formula is a state formula, you may first replace the subformulas starting with E or A by new propositional variables. If that is done, and a propositional logic formula is obtained, you have a state formula, otherwise it is a path formula since subformulas with temporal operators are left.
Third, I guess you don't understand the nesting of automaton formulas. An automaton formula A(Q,I,R,F) is evaluated on a path and either accepts or rejects the path by evaluating the acceptance condition F which is a path formula on the path (in a product structure). Automata formulas themselves are also path formulas, so we can consider A(Q1,I1,R1,A(Q2,I2,R2,F2)) which is equivalent to A(Q1∪Q2,I1∧I2,R1∧R2,F2) and the latter is simply the product automaton of the two involved automata. You can find that in the omega-automata chapter.