Problem 7a
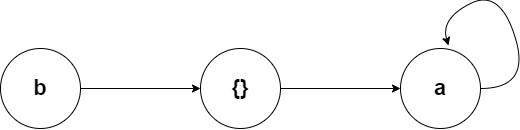
Provided above is the counterexample that I came up with and given below is the LTL for this counterexample structure
((!a & b) & X(!a & !b) & X(G a))
which seems to satisfy S1 and not S2
S1 = b & X (!b & G F a)
S2 = b & X (!b & G a)
Given below is the input that I gave to the LTL teaching tool.
((!a & b) & X(!a & !b) & X(G a)) -> (b & X (!b & G F a)) & !(b & X (!b & G a))
It returns valid for this combination, however it returns valid for all the other combinations given below:
((!a & b) & X(!a & !b) & X(G a)) -> !(b & X (!b & G F a)) & (b & X (!b & G a))
((!a & b) & X(!a & !b) & X(G a)) -> !(b & X (!b & G F a)) & !(b & X (!b & G a))
((!a & b) & X(!a & !b) & X(G a)) -> (b & X (!b & G F a)) & (b & X (!b & G a))
Is the counterexample structure and the corresponding LTL correct? If so, why does the teaching tool return "VALID" for all the rest of the combinations?