Do you know Frank Stockton's story "The Lady or the Tiger?," in which the prisoner must choose between two rooms, one of which contains a lady and the other a tiger. If he chooses the former, he marries the lady; if he chooses the latter, he (probably) gets eaten by the tiger.
The king of a certain land had also read the story, and it gave him an idea. "Just the perfect way to try my prisoners!" he said one day to his minister. "Only, I won't leave it to chance; I'll have signs on the doors of the rooms, and in each case I'll tell the prisoner certain facts about the signs. If the prisoner is clever and can reason logically, he'll save his life-and win a nice bride to boot!"
"Excellent idea!" said the minister.
I'll put a lady in one room and a tiger in each of the other two rooms. Then we'll see how the prisoners fare!"
"Excellent ideal" replied the minister.
"Your conversation, though flattering, is just a hit on the repetitious side!" exclaimed the king.
"Excellently put!" replied the minister.
The king did as planned. He offered three rooms to choose from, and he explained to the prisoner that one room contained a lady and the other two contained tigers. Moreover, the king explained that at most one of the three signs was true. Which room contains the lady? Here are the three signs:
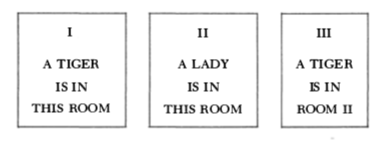
Now, how can that be formulated in propositional logic, and maybe as a BDD that will show us the answer?
Side remark: Take my apologies for quoting a puzzle that stems from a time, where gender policies were not really in peoples' minds. Of course, not all prisoners are men, and ladies should not be treated as their awards.