A Propositional Logic Puzzle

Question

Here is a puzzle (stolen from a logic textbook that I appreciate) that can be solved by BDDs or other methods for propositional logic learnt in VRS, can you?

Three subjects (don't want to say men or women) - A,B, and C - were all perfect logicians. Each one can instantly deduce all consequences of any set of premises. Also, each was aware that each of the others was a perfect logician. The three were shown seven stamps: two red ones, two yellow ones, and three green ones. They were then blindfolded, and a stamp was pasted on each of their foreheads; the remaining four stamps were placed in a drawer. When the blindfolds were removed, A was asked, "Do you know one color that you definitely do not have?" A replied, "No". Then B was asked the same question and replied "No". Is it possible, from this information, to deduce the color of A's stamp, or of B's, or of C's?

Note that satisfiability of your formula is not enough, since you have to make sure that whatever you deduce from the facts holds on all models of the facts. So, can anybody solve this?

Comments

A can neither have seen B:red/C:red, B:yellow/C:yellow. (otherwise A could exclude this color)

B has also neither seen A:red/C:red, A:yellow/C:yellow. Furthermore, C:yellow and C:red have not been seen by B (otherwise B would exclude these for themselves)

So I definitely know that C is green.

Now put that into formal logic. Good luck.

---

Okay, I will add the solution now with propositional logic. You found it already by thinking about the problem.

Answer 1

Here is a solution of the above problem that I created using the following variables:

• redA/yellowA/greenA: A has a red/yellow/green stamp
• redB/yellowB/greenB: B has a red/yellow/green stamp
• redC/yellowC/greenC: C has a red/yellow/green stamp
• excludeRedA/excludeYellowA: A can exclude the possibility to have a red/yellow stamp
• excludeRedB/excludeYellowB: B can exclude the possibility to have a red/yellow stamp

The important point here is that we have knowledge about what we know like "A has a red stamp" etc. but also what A and B don't know. For this reason, we use variables excludeRedA etc. to express this. Note that it is impossible for anyone to exclude color Green, so we don't use such variables for that color.

However, if one can see two red stamps on the others' heads, it is clear that the own stamp can no longer be a red one since only two red stamps exist. Same with the yellow one. Since A cannot exclude any color, we can conclude that A does neither see two red stamps nor two yellow stamps on B and C's heads. Thus, if redC holds, then excludeRedA must hold.

Now, here is the entire formula:

// each one of A,B,C has a stamp on the head
(redA | yellowA | greenA) &
(redB | yellowB | greenB) &
(redC | yellowC | greenC) &
// and each one has no more than one stamp on the head
(redA -> !greenA & !yellowA) &
(greenA -> !redA & !yellowA) &
(yellowA -> !redA & !greenA) &
(redB -> !greenB & !yellowB) &
(greenB -> !redB & !yellowB) &
(yellowB -> !redB & !greenB) &
(redC -> !greenC & !yellowC) &
(greenC -> !redC & !yellowC) &
(yellowC -> !redC & !greenC) &
// there are only two red stamps
(redA & redB -> !redC) &
(redB & redC -> !redA) &
(redA & redC -> !redB) &
// there are only two yellow stamps
(yellowA & yellowB -> !yellowC) &
(yellowB & yellowC -> !yellowA) &
(yellowA & yellowC -> !yellowB) &
// How to exclude a color is the challenge: A can exclude color red
// if A can see that B and C have red colors (since there are only
// two stamps with red color), but also if C has a red color, and B
// cannot exclude red color. Note that redC & !excludeRedB implies
// redC & !redA & excludeRedA), so that A can exclude color red.
// The same applies to color yellow, but note that there is
// no way to exclude color green.
(redB & redC or redC & !excludeRedB -> excludeRedA) &
(redA & redC or redC & !excludeRedA -> excludeRedB) &
(yellowB & yellowC or yellowC & !excludeYellowB -> excludeYellowA) &
(yellowA & yellowC or yellowC & !excludeYellowA -> excludeYellowB) &
// neither A nor B can exclude a color
!excludeRedA & !excludeYellowA &
!excludeRedB & !excludeYellowB

These are quite many variables so that truth tables are no longer fun. You can of course, reason about the above clauses manually, which will quickly lead to some solution (try it). Instead, I rather computed a ZDD (left hand side) and a BDD (right hand side) for it and got the following results (ZDDs are always good for puzzles):

                        

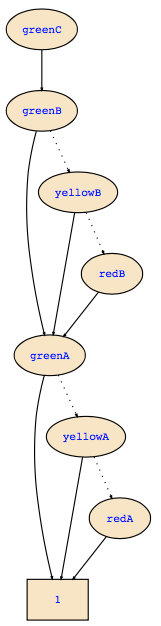
Since the BDDs show all models of the formula, you can now see that in all models greenC is true, but for A and B, we don't know. 

Without BDDs, you can also use the SAT solver to check whether it can prove that one of A, B, C must have one color. Calling the above formula Φ, we check  Φ & !greenC for satisfiability (which should not be the case to prove validity of Φ ➞ greenC). And, of course, here is what my SAT solver says (I skipped the listing of the clauses):

computed the following clauses:
      redC&redA&redB -> false
      redA&__def3 -> false
      yellowC&yellowA&yellowB -> false
      :
      :
--------------------------------------------------
DecisionStack: 
--------------------------------------------------
atom redC := False 
propagated atoms:
    made 0: __def13,excludeRedA,excludeRedB,excludeYellowA,greenC,redC
    made 1: __def12,__def15,__def17,__def19,__def23,__def31,__def32,__def33,excludeYellowB,yellowC
DecisionStack: 
    redC := False 
computed assertion clause excludeYellowB -> false by uips ?,__def32,__def33,excludeYellowB,redC,yellowC of 18 :{excludeYellowB -> false}
got assertion clauses 
all learnt clauses are already known
--------------------------------------------------
backtracked to the following decisions
DecisionStack: 
    redC := True (only choice)
computed assertion clause excludeRedB -> false by uips ?,__def24,__def25,excludeRedB,redC of 14 :{excludeRedB -> false}
got assertion clauses 
all learnt clauses are already known
--------------------------------------------------
backtracked to the following decisions
DecisionStack: 
-------------------------------------------------------
no model
-------------------------------------------------------