If a holds at t=0, but not afterwards, then Fa holds at t=0, but also no more at t>0, so it is no longer true then. F-properties are always of that kind. If they hold at t=0, then they also may hold for some time, and then switch to false for the rest of time (or keep true forever). The point of time where Fφ will switch to false is the last point of time where φ holds (if there is such a point of time). If φ holds infinitely often, then Fφ is always true. If φ holds never, then Fφ is always false.
A general remark to answer these kinds of questions: You can draw a Kripke structure with a single infinite path so that the distinction on E and A quantifiers does not matter. Then you can check even the LTL properties by adding E/A quantifiers in front of every temporal operator so that you can use our CTL model checker to answer the questions you have.
For your example, I would have drawn the following structure:
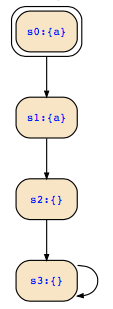
Input for the CTL model checker would be as follows:
vars a,b;
init 0;
labels 0:a; 1:a; 2:; 3:;
transitions 0->1; 1->2; 2->3; 3->3;
and here you may let the model checker compute the following for you:
- 〖E F a〗= {s0;s1} =〖a〗
- 〖E[(E F a) WU b]〗= E[a WU b]〗= {}
- 〖E G b〗= {}
- 〖E[false SU a] =〖a〗= {s0;s1}
Please note that in general, the formulas checked here are not the same, but on structures with only a single infinite path, there is no distinction between CTL/CTL*/LTL and neither between E and A. For past operators, that is however not the case. Still, in many cases single paths are sufficient to distinguish between formulas, and then the above approach gives you quickly reliable answers.