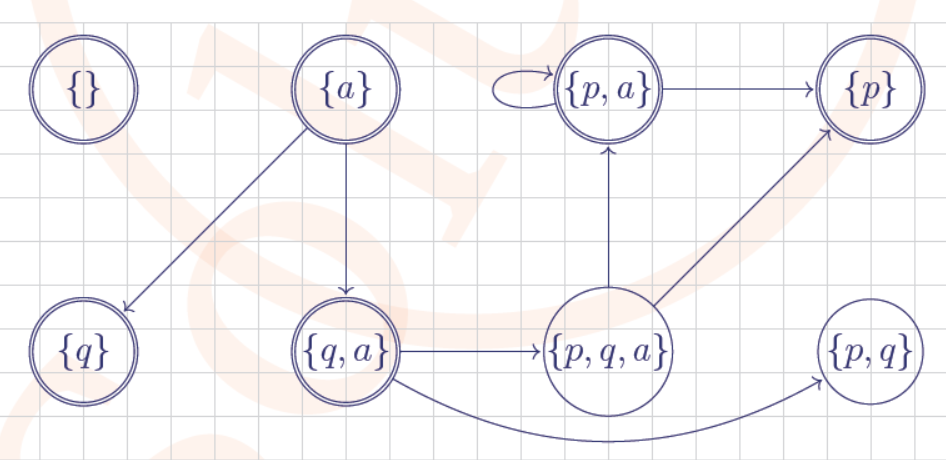

I am getting confused. For showing property phi is inductive,
we first take all the states that satisfy phi. Example here, {{p,a}, {p},{p,q,a},{p,q}}
then find universal predecessor of phi ({p,a}, {p},{p,q,a},{p,q}, {q,a})
then check if phi is subset of universal predecessor of phi. if yes then property is inductive else not.
But I don't understand why we are looking here for successors? I know the lemma where exsitential successors of Q1 is subset of Q2 (lecture 9- slide 12), but I really don't understand what is Q1 and Q2 referring to in this example.