Consider the Co-Büchi automaton with a set of inputs Σ=Σ={{a},{}}, the state variables state=Vstate={q0,q1}, the initial condition φI=!q0&!q1|q0&q1, the acceptance condition (q0&!q1|q1&!q0), and the following state transition diagram:
The given automaton:
inputs {a},{};
outputs ;
init 0,3;
transitions (0,{},,2);(1,{a},,2);(2,{a},,3);(2,{},,2);(3,{a},,0);(3,{a},,1);
accept 1,2;
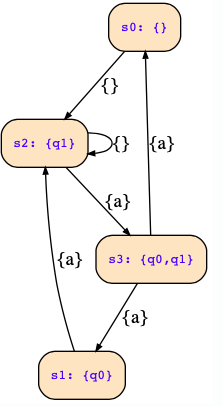
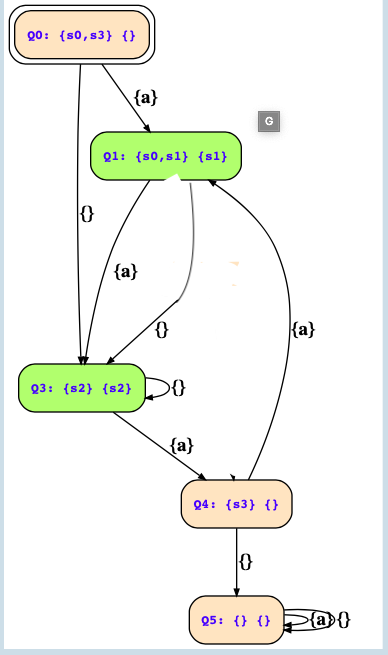
This is my solution which is incorrect as "Q2" is missing with Qf = {} (Please see the following image for the correct answer as per the tool).
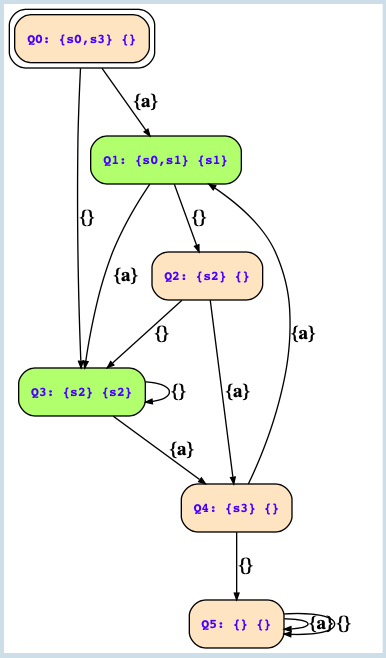
This is the correct solution as per the tool.

My questions:
1. Can someone please explain why was the state "Q2" with (Q,Qf) = (s2 , {}) is present in the final solution?
2. The formula in OmegaAutomata slide# 90, states the condition only for the input \sigma, does that \sigma also means an empty input?
3. I am confused with the "Otherwise" condition in the formula on slide#90. Can you please give an example of the "otherwise" condition i.e., when Qf ≠ {}. Other variants I solved, didn't have duplicate states like in this variant.
Thank you in advance.