Well, you must first read the chapter on induction, i.e. VRS-09-Induction before you are ready for this kind of exercise. In particular, you will find the PDR method on pages 98-100, but to understand that, you need the really many slides before (depending in which detail you want to understand it). It is impossible to summarize those 100 slides here in a few lines.
Looking at the exercise, the first thing I notice is that your transition relation is not correct. The generated transition system does not look like yours. Instead, the transition relation should be as follows:
a&!b&!c & !next(a)&!next(b)& next(c) |
!a&!b& c & next(a)&!next(b)&!next(c) |
!a& b&!c & next(a)& next(b)&!next(c) |
a& b&!c & next(a)&!next(b)& next(c) |
a&!b& c & !next(a)& next(b)& next(c) |
!a& b& c & next(a)& next(b)& next(c) |
a& b& c & !next(a)& next(b)&!next(c)
and will give you the following Kripke structure:
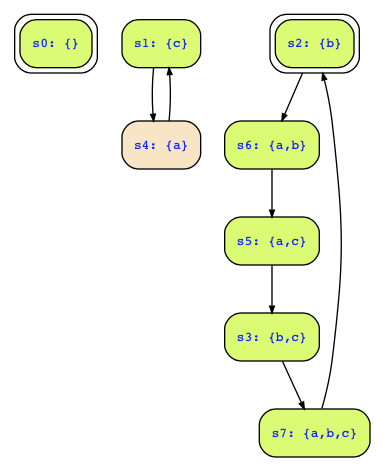
Initial states are !a&!c, so that the reachable states are s0,s2,s3,s5,s6,s7, i.e., all states but s1 and s4. The safety property phi to be checked is b|c|!a which holds in all states except for s4 (these are the green states).
Hence, the property is not inductive, since there are states (namely s1) where phi holds but where some successor state does not satisfy phi.
Hence, we cannot prove this property by applying the simple induction rule even though all reachable states satisfy phi, and therefore AGphi holds on all initial states. Instead, we have to strengthen the induction property until we find a stronger property that is inductive. PDR does this automatically.
To this end, PDR starts as follows with the following initial checks:
(1) Check the Safety of Initial States I(x) ➞ Φ(x), i.e., check whether all initial states are included in the safety property. In our case, all initial states satisfy the safety property, so there is no counterexample of length 1.
(2) Check the Safety of the Successors of Initial States I(x) ⋀ R(x,x') ➞ Φ(x'), i.e., check whether all successor states of all initial states satisfy the safety property. In our case, all successors of initial states satisfy the safety property, so there is no counterexample of length 2.
(3) Check the Inductiveness of Initial States I(x) ⋀ R(x,x') ➞ I(x'), i.e., check whether all successor states of all initial states are also initial states. If that would be true, the initial states would be the reachable states. However, in our case that is not true, since we have a transition s2->s6 from the initial state s2 to a non-initial state s6.
(4) Check the Inductiveness of the Safety Property Φ(x) ⋀ R(x,x') ➞ Φ(x'), i.e., whether all successors of green states are green states. In our example, this is not the case, since we have for example, s1->s4 and while s1 satisfies the safety property, s4 does not. Hence, we don't get a cheap proof this way.
Hence, the initial checks were not conclusive, we can neither prove nor disprove the safety property with the simple checks (1)-(4) and therefore PDR has to start its work.
PDR will therefore check the counterexample to the induction step which is only the transition s1->s4. PDR will then find out that s1 is not reachable and will remove s1 from the green states. Checking inductiveness again will then work, and a proof is found with the stronger safety property {s0,s2,s3,s5,s6,s7} which can be expressed as ¬a&¬c ∨ b ∨ a∧c. This is inductive and it implies the given property.
For more details, you really have to study the chapter on induction, it is quite involved and cannot be summarized here in a few lines of text.