[DOUBT] CTL model checking from Exercise 12

Question

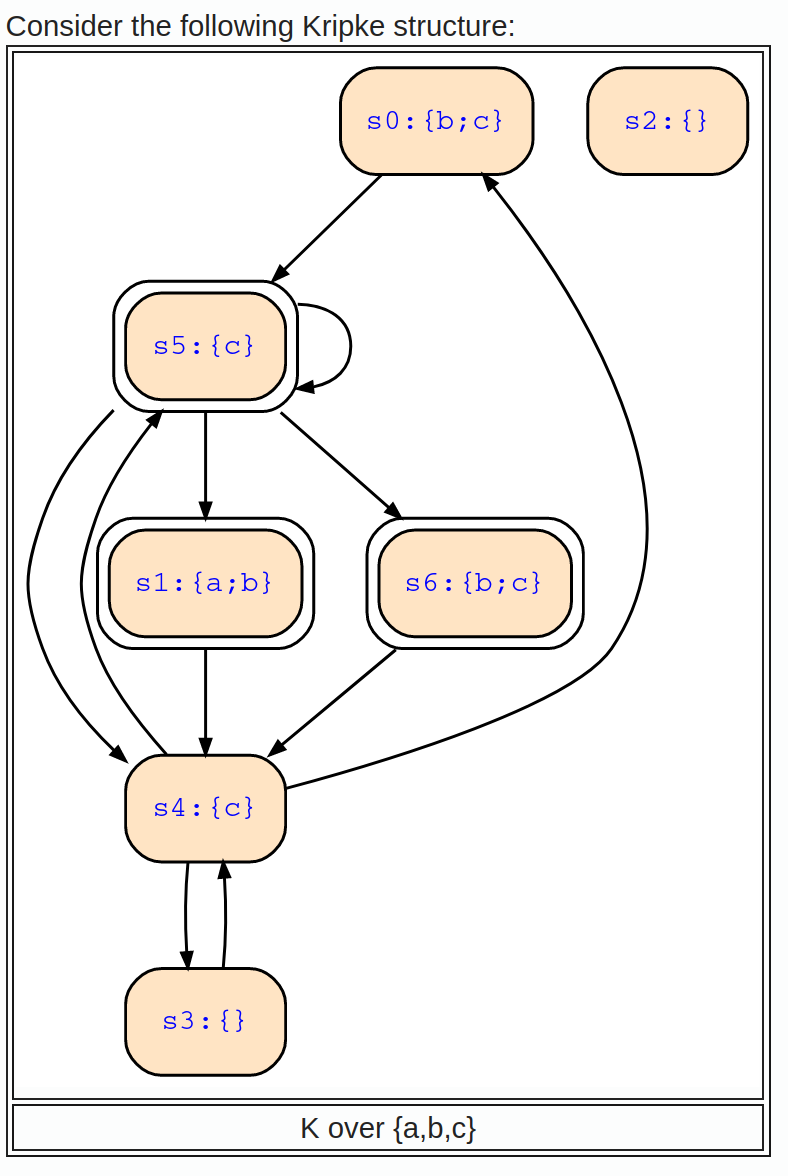
I am unable to interpret how the below formula works for CTL model checking.

S4=A F b | E [a SU a]

The answer received from the tool is: {s0;s1;s2;s6}.

However, I got the following states when I tried computing:

a = {s1}; (i.e., a is true only in s1)

E[a U a] = {s1}; (i.e., run where a U a holds)

Fb = {s0, s1, s3, s4, s5, s6}; (i.e., There is an infinite path (s0 to s4 and back to s0), starting from s0, which makes sure Fb is true at s0 and traversal through s0 via all states will still satisfy Fb).

AFb = {s0, s1, s2, s3, ..., s6} (i.e., Every run will eventully reach Fb states and s2 satisfies trivially.)

Hence, I end up with the answer, i.e., E[a U a] | AFb = {s0, s1, s2, s3, ..., s6}

Kindly request some help in understanding where I'm going wrong. Also, thanks in advance for all the support given so far.

Answer 1

I don't understand your argumentation about AF b, and I think that you are confused with EFb and AFb. Also, Fb is a path formula so that is does not make sense to reason about the set of states where Fb holds. 

You may argue that the states {s0, s1, s3, s4, s5, s6} form a strongly connected component so that any state in this set can be reached by any other state in this set. Since one of these states satisfies b, you can argue this way that EF b = {s0, s1, s3, s4, s5, s6}, but AFb is another thing. 

The teaching tool explains that clearly. AFb is µZ.(b | []Z) so that the fixpoint computation is done as follows:

    〖b〗= {s0;s1;s6}
    step 0 : Z = {}
        〖Z〗= {}
        〖[] Z〗 = {s2}
        〖b | [] Z〗 = {s0;s1;s2;s6}
    step 1 : Z = {s0;s1;s2;s6}
        〖Z〗= {s0;s1;s2;s6}
        〖[] Z〗 = {s2}
        〖b | [] Z〗 = {s0;s1;s2;s6}
        〖Z〗= {s0;s1;s2;s6}

Hence, the fixpoint computation starts with b-states and deadend states, and adds universal predecessors until a fixpoint is reached.

Comments

This is where i was going wrong! My understanding about AF wasn’t correct. Thanks for the correction.!

Just out of curiosity, looking at it through intuition point of view, could we say AFb cannot contain s5, s4, and s3 because one of the runs i.e., getting stuck infinitely b\w s3, s4, and s5 would never reach states where b holds?

---

Absolutely right, that is the case.

---

Understood. Totally makes sense now. Thanks again.