Question from exercise:

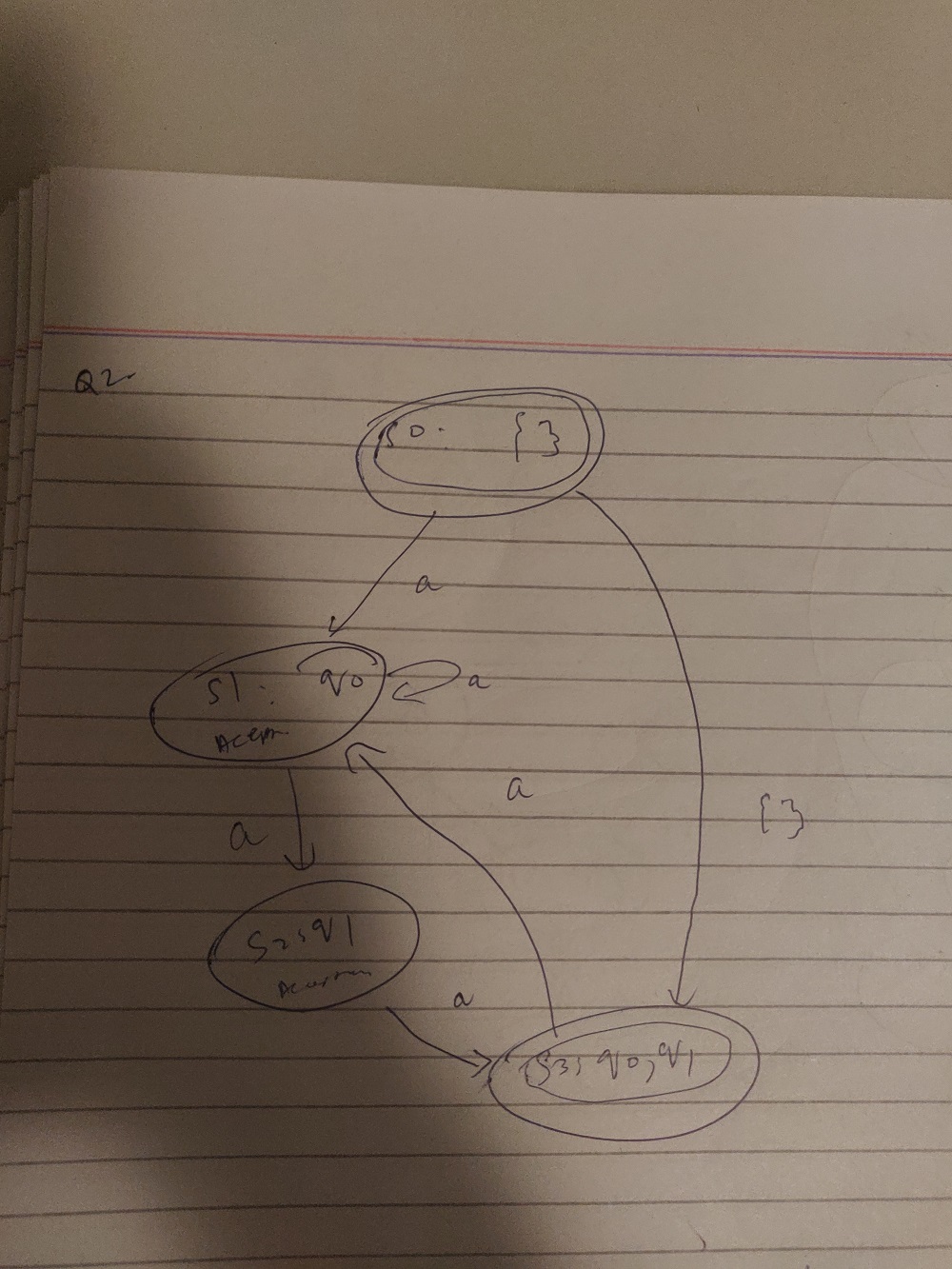
My construction as first step:
My Final construction:
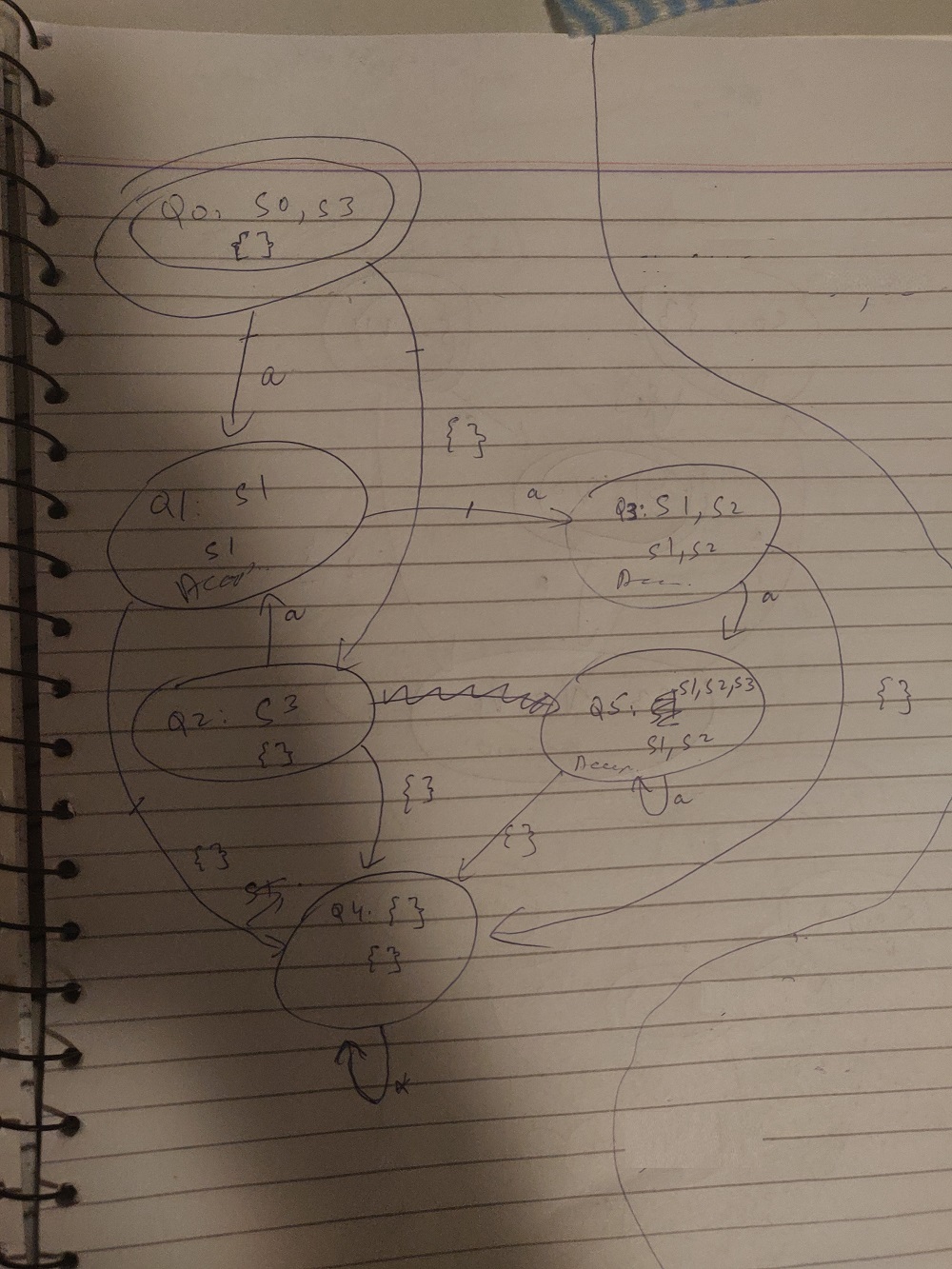
My answer for this was
labels 0:s0,s3; 1:s1; 2:s3; 3:s1,s2; 4:; 5:s1,s2,s3; // encode Q
labels 0:; 1:s1; 2:; 3:s1,s2; 4:; 5:s1,s2; // encode Qf
init 0;
transitions (0,{a},,1); (0,{},,2); (1,{a},,3); (1,{},,4); (2,{a},,1); (2,{},,4); (3,{a},,5); (3,{},,4); (5,{a},,5); (5,{},,4); (4,{a},,4); (4,{},,4);
accept 1,3,5;
This answer was accepted.
My question is related to type of automaton.
G: Safety Automata: it means always in accepting state.
F: Liveness Automata: it means eventually visit an accepting state at least once.
FG: Co-Büchi Automata: always visit an accepting state.
GF: Büchi Automata: final state must be accepting state.
If I am given just an automaton like the one, I drew in my first step. How can I determine the type of automaton from that?
Thank you in advance!