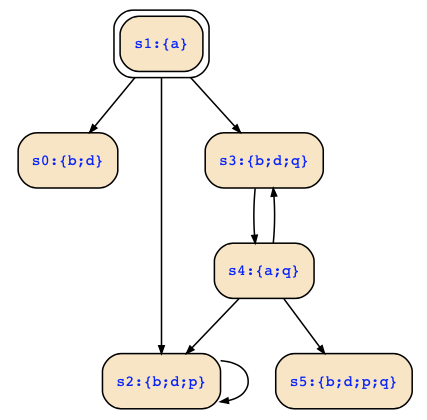
I have added two additional variables p,q to uniquely identify the states so that I have the following Kripke structure:
vars a,b,d,p,q;
init 1;
labels
0:b,d; 1:a; 2:b,d,p;
3:b,d,q; 4:a,q; 5:b,d,p,q;
transitions
1->0; 1->2; 1->3; 2->2; 3->4; 4->2; 4->3; 4->5; which looks as follows:
Using our model checker, it computed the universal predecessors of s3,s4, i.e.
[](!a&b&d&!p&q | a&!b&!d&!p&q)
as follows:
〖!a & b & d & !p & q〗 = {s3}
〖a & !b & !d & !p & q〗 = {s4}
〖!a & b & d & !p & q | a & !b & !d & !p & q〗 = {s3;s4}
〖[] (!a & b & d & !p & q | a & !b & !d & !p & q)〗 = {s0;s3;s5}
Hence, pre∀({s3,s4}) = {s0,s3,s5}.
The universal successors of {s3,s4} are computed as follows:
〖!a & b & d & !p & q〗 = {s3}
〖a & !b & !d & !p & q〗 = {s4}
〖!a & b & d & !p & q | a & !b & !d & !p & q〗 = {s3;s4}
〖[:] (!a & b & d & !p & q | a & !b & !d & !p & q)〗 = {s1;s4;s5}
Hence, suc∀({s3,s4}) = {s1,s4,s5}.
Without the dashed transition, I also computed pre∀({s3,s4}) = {s0,s3,s5} and suc∀({s3,s4}) = {s1,s4,s5}.