Consider the following symbolic representation of a FSM: A=(2Vin,2Vout,φI,2Vstate,φR)A=(2Vin,2Vout,φI,2Vstate,φR), where Vin={a}Vin={a}, Vout={o}Vout={o}, Vstate={p,q}Vstate={p,q}, φI=p∨qφI=p∨q, φR=φR=!((next(q)->p)<->(o&q->a))&next(p)
a) Compute the existential predecessors of !(a|a) for the corresponding Kripke structure of the FSM.
b) Compute the universal predecessors of !(a|a) for the corresponding Kripke structure of the FSM.
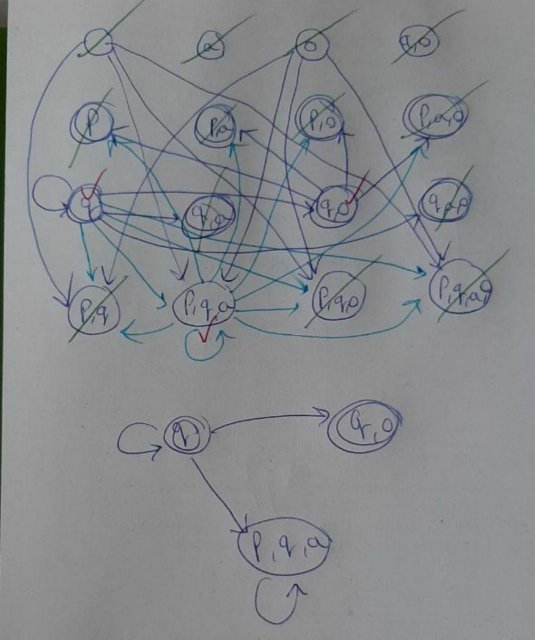
for this question as far as I understood, we need to first create the Kripke out of FSM. But what are the next steps?
Here I have the Kripke (if I calculated it correctly). What should I do next?