Local Model checking Aug 2017 que 5

Question

In this que, for the given kripke, if i consider the path s6->s0->s3->s2 i can satisfy the condition

b V Predecessor(X).

But Why was that not considered in the solution but ended up with s6->s0 looping around without satisfying the condition?

Answer 1

The short answer is: The loop at s0 does satisfy the condition. (See slide 89 on in the µ-calculus chapter)

If there is a loop at ν, we consider is satisfied. If the loop is a µ, we don't. Hence, the loop at loop at s0 satisfies our diamond.Since a diamond needs to be satisfied just once, we are done.

Of course, it is also possible to first check s2 and then s3. But the single step of just following the selfloop sufficed in fewer steps. That's why this variant was chosen by the online tool.

Answer 2

I am not sure whether I understood the question, but let me try to explain. I guess you consider problem 5a of that exam, where you should check which states satisfy nu x. (b | <>x). This formula does not really require a fix point computation since (1) x is initialized by true for computing greatest fixpoints, and (2) <>true holds on all states that have a successor state, i.e., on all states of the Kripke structure in that example. Thus, b | <>x are still all states, and that is the final fixpoint. 

Doing local model checking for checking s6 ⊢ nu x. (b | <> x) will reduce to checking s0 ⊢ nu x. (b | <> x) which "justifies itself": Since s0 is a successor of itself, there is a disjunctive branch in the local model checking tree to the same goal s0 ⊢ nu x. (b | <> x) again which is sufficient to prove a greatest fixpoint.

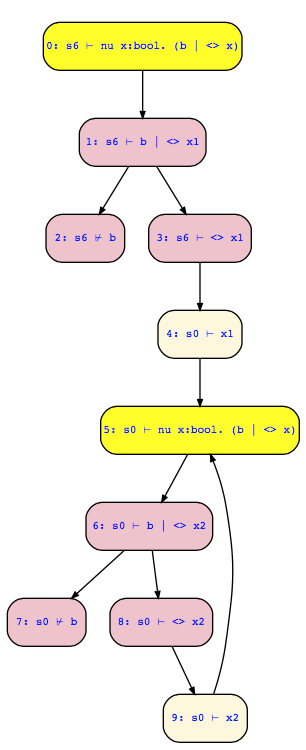
Note here that in node 8 we have to check whether for one of the successor states of s0 our fixpoint formula holds. The tool luckily found first successor state s0 which satisfies it. You may first check any other successor state, and then the solution may look differently, but may still be correct. 

You can select in the new teaching tool the conversion to a parity game which essentially does local model checking in a non-lazy way, i.e., exploring all subgoals even those not needed for local model checking. That should then include your solution, where the fixpoint is checked in s0, s3, s4, and s6. Maybe that is what you did?