The following does not yield an explanation for how we generally multiply with B-Complement numbers, but I think the misunderstanding here comes from not evaluating the digits the right way. That's why I'll focus on explaining your last question.
"How does the table yield -1 as carry?"
As is explained in Chapter 2 - slide 102, you want to apply the function alpha to the first digit of a B-Complement number.
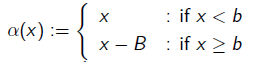
with b = B/2.
Thus the first digit of each of these numbers is read as -1 since for x = 1, x >= b holds and x - B = 1 - 2 = -1.
This means that for each row in the leftmost cell we don't calculate x*1 but x*α(1) = x*(-1).
This also applies in the lowest row for each calculation 1*y, where we calculate α(1)*y = (-1)*y.
Now let's look at the leftmost cell of the first row. We calculate 1*(-1) = -1.
Since -1 is not a valid digit we have to find an alternative representation. In 2-Complement this would be <11>2 (note that the first digit represents -1 due to reasons discussed above). So we get 1 as resulting digit (edge below the cell) and -1 as carry (edge to the left).
In the next two rows we see that the result of the computation is 0 respectively, but adding our carry of -1 we yield -1 as result once again. The same step as described above is therefore applied and the carry of -1 moves further to the left.
In the last row the calculation is (-1)*(-1) due to reasons discussed above. Therefore the result is 1. We add our carry of -1 and yield 0. That's why at this point we get 0 as digit and 0 as carry.