You need the following images to follow the computation:
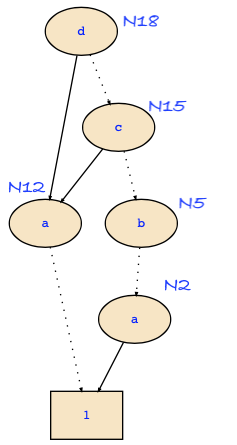
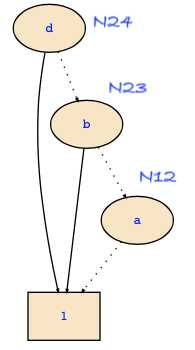
It is not straightforward to read the output of the tools since the sequence of operations is not directly the way it has been computed. The reason for this is that BDD tools use a computed table and don't compute things twice. In the example, the computation starts with Restrict(N_18,N_24):
(1) Restrict(N_18,N_24)
= (d ? Restrict(N_12,N_1) : Restrict(N_15,N_23))
Hence, we now compute (2) Restrict(N_12,N_1) = N_1
Note that there is already a node N_1, of course. We then continue with
(3) Restrict(N_15,N_23)
= Restrict(OR(N_5,N_12),N_23)
so that we have to compute
(4) OR(N_5,N_12)
= (b ? OR(N_0,N_12) : OR(N_2,N_12))
and now
(5) OR(N_0,N_12)
= (a ? OR(N_0,N_0) : OR(N_0,N_1))
= (a ? N_0 : N_1)
= N_12
Note that a node (a ? N_0 : N_1) already exists and this is N_12. So, we don't have to create a new node and can use an existing one. We continue with the second part of (4)
(6) OR(N_2,N_12)
= (a ? OR(N_1,N_0) : OR(N_0,N_1))
= (a ? N_1 : N_1)
= N_1Clearly, N_1 is already there, so that we can now finish (4) as follows:
(4) OR(N_5,N_12)
= (b ? OR(N_0,N_12) : OR(N_2,N_12))
= (b ? N_12 : OR(N_2,N_12)) // by (5)
= (b ? N_12 : N_1) // by (6)
=: N_25
The BDD package has to create a node (b ? N_12 : N_1) for this BDD since such a node does not yet exist. It therefore creates at address 25 (which was the next free one) a new node for (b ? N_12 : N_1).
Now, we continue with (3)
(3) Restrict(N_15,N_23)
= Restrict(OR(N_5,N_12),N_23)
= Restrict(N_25,N_23)
= (b ? Restrict(N_12,N_1) : Restrict(N_1,N_12))
= (b ? N_1 : N_12)
= N_23
A node (b ? N_1 : N_12) is already there, it is N_23 that we an reuse here. Now, we don't need N_25 no more, but it was needed during the computations. That is not uncommon, and therefore BDD packages need garbage collection to remove such garbage nodes afterwards. However, for a while they might still be useful (in case such a node needs to be created again).
The completion of (1) is now simple:
(1) Restrict(N_18,N_24)
= (d ? Restrict(N_12,N_1) : Restrict(N_15,N_23))
= (d ? N_1 : N_23) // by (2) and (3)
= N_24Note that a node (d ? N_1 : N_23) already exists under address N_24.
So, the answer is that the node N_25 was generated and needed during the computation, but was later on not needed anymore and is therefore garbage at the end. You may also wonder about other addresses like N_4, N_6 and so on that are not shown in the images. However, they were also needed at some time to compute the BDDs rooted in N_18 and N_24 where our computation started with.