There are already a couple of answers that should clarify the situation. Anyway, let's summarized: You were given the following decision diagram:
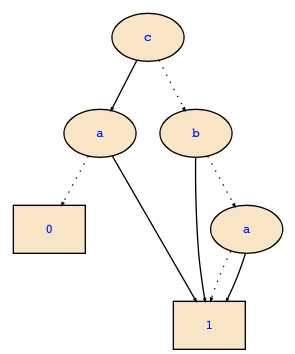
It may be a FDD or a ZDD, but for sure it is not a BDD since there a node labelled with a that has the same cofactors which is impossible for BDDs. The exercise question says that you should first compute the set representation which is the same for FDDs and ZDDs, and you have done that correctly and obtained
{{a,c},{a},{b},{}}
Looking again at the exercise sheet, you should interpret this decision diagram now as a FDD and should this way derive the represented formula. To make it simple, you should represent the formula in RMF. Your formula is therefore the following one
a&c ⊕ a ⊕ b ⊕ true
Now you should convert this formula to a ZDD. You will find the following result:
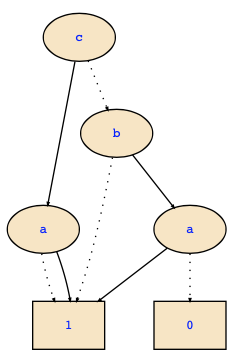
It is the same formula, but given now as a ZDD instead of a FDD. Again, you should derive the set representation of this decision diagram which is now
{{a,b},{a,c},{c},{}}.
Does this help?