I have a question regarding the Exists-algorithm:
Let Φ be a&c&!b|a&!b&!c|b&c|b&!a&!c
Then the ROBDD of Φ is
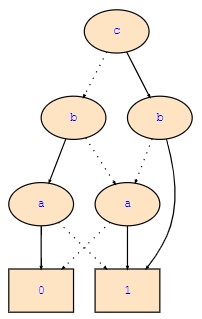
I'm now trying to compute Exists(X,¬Φ) with X = a&d.
The ROBDD of ¬Φ ist just the ROBDD of Φ with 0 and 1 swapped.
If I understand correctly, applying the Exists algorithm Exists(X, ¬Φ) is equivalent to asking ourselves the question "Are there variable assignments satisfying ¬Φ with a=1, d=1?"
Therefore, the algorithm outputs a graph which shows us variable assignments v (with a=1, d=1) satisfying ¬Φ.
Therefore, we should be able to solve the question by just taking a look at the ROBDD of ¬Φ and just "deleting" all arrows starting from {a, d} representing the "false" path (as shown in the picture, deleted paths in red) because these paths are not possible since we know that a, d have to evaluate to TRUE:
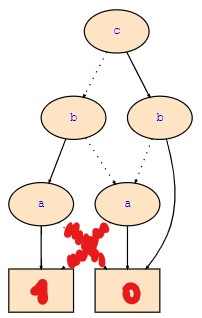
Now, I transform this into an ROBDD:
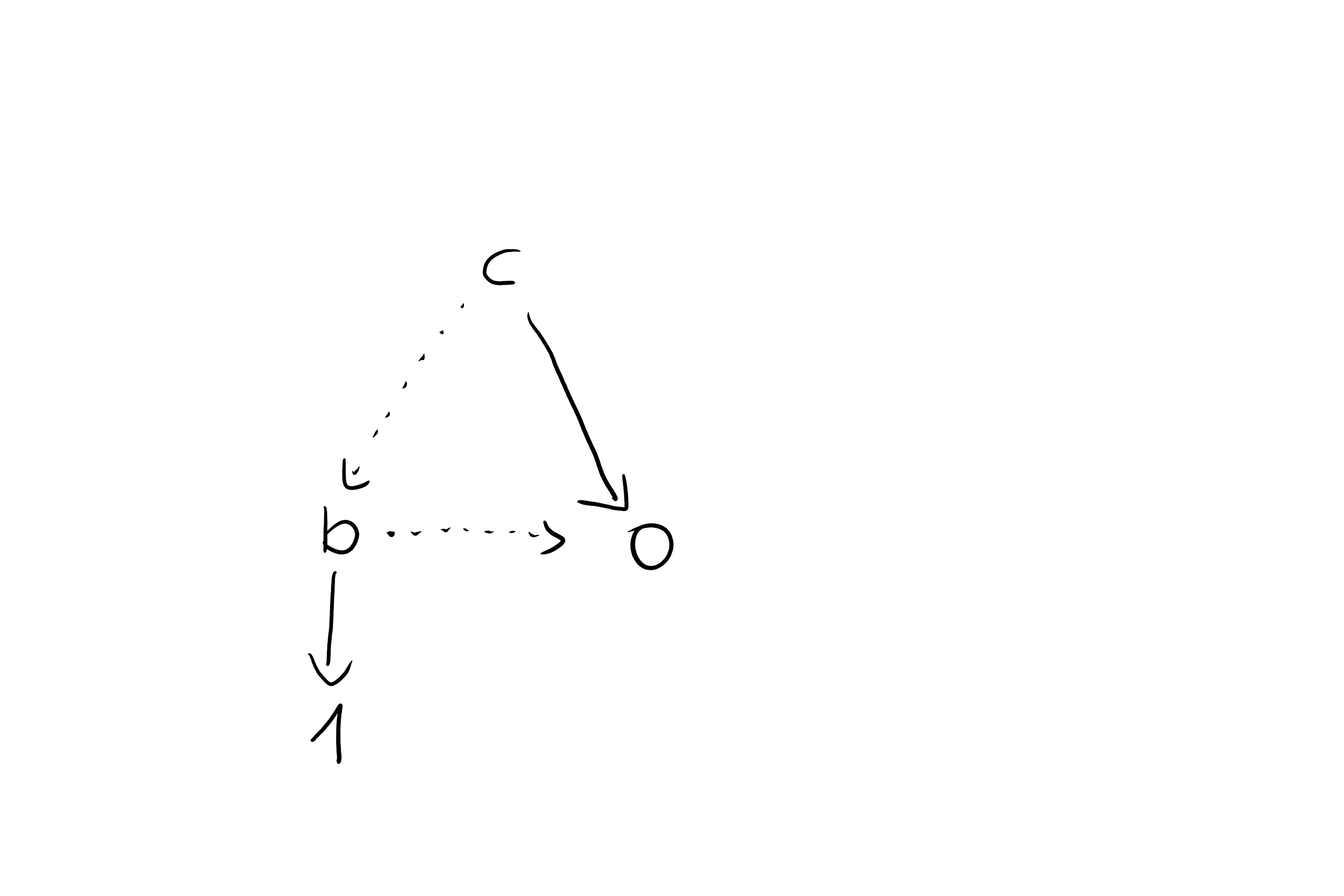
However, this is supposedly wrong (according to the StudentPortal) and the correct solution looks like this:
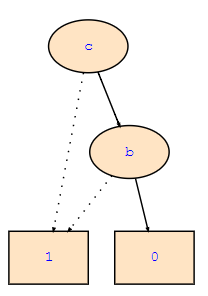
In which step is my solution wrong?