The highest rank we see in the original game is certainly 9, and since this is an odd number, the winner with the highest rank is player 1. The highest rank states are Qh := {s2}, and the attractor set is A := attractor(1,Qh) := {s0,s1,s2,s5,s6}. In these states, player 1 can force states of rank 9 to be reached and win the game. However, we have to make sure that player 0 cannot escape in the remaining states, so we consider the game G\A without attractor A.
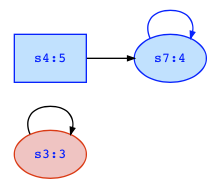
This game consists only of the states s3,s4,s7. Without further calculations it is easy to see that in states s4 and s7 there is only one infinite path, which loops infinitely often in s7, which has rank 4. Therefore player 0 wins in states s4 and s7. In state s3 there is only one self-loop, and since s3 has rank 3, player 1 wins in s3. So the winning states are win1={s3} and win0={s4,s7}. With this result we can return from the recursion and finish the above computation. Of course, you can also compute this result formally, but I think it is obvious, since there is only one infinite outgoing path in each state, and the players have no choices. The player with the highest rank on that path is the winner on those paths (and the states where those paths start).
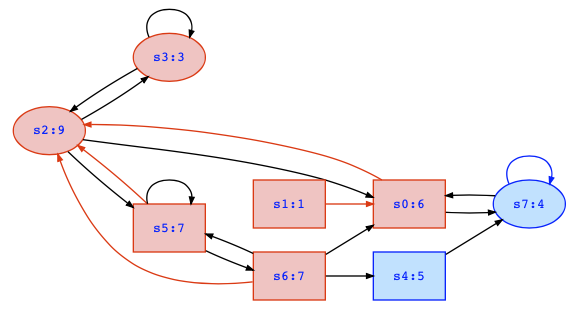
So, what do we know now? We know that if we are in states {s0,s1,s2,s5,s6}, player 1 can enforce reaching state s2 with rank 9, and if the game should then switch to win1={s3}, it would neither be harmful for player 1 if we would remain there, nor if we would return to state s2, i.e. states {s0,s1,s2,s5,s6} where player 1 can again enforce to reach s2. The only problem for player 1 could be that the game play may leave states {s0,s1,s2,s5,s6} to win0={s4,s7} without returning to {s0,s1,s2,s5,s6}. For this reason, we have to compute B := attractor(0,win0) := {s4,s7} since in these states, player 0 can enforce reaching win0 and will thus win there.
Do you agree?