Look at the definition of the relation H{i+1}:
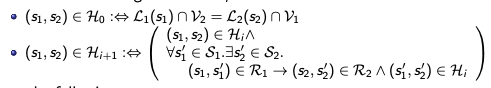
Instead of
∀s1'∈S1.∃s2∈S2. (s1,s1')∈R1 ⟹ (s2,s2')∈R2 ⋀ (s1',s2')∈H{i},
we can equivalently write
∀s1'∈S1. (s1,s1')∈R1 ⟹ ∃s2∈S2. (s2,s2')∈R2 ⋀ (s1',s2')∈H{i}.
Now, if we have a state s1 that does not have a successor state, the left part of the implication is false for all states s1'∈S1, and therefore the implication is true. That is the reason why the pair (Q3,S0) survives in all relations H{i}.