Well, maybe your cheat sheet is not sufficient?
The equivalence G!b = A∃({a},q,!b&b&next(q),true) holds, since the state {q} is the initial state and the only reachable state of the automaton. It has a self-loop which is enabled if b is false. So, there is an infinite run for a word if and only if b is always false. Hence, the automaton is equivalent to G!b. If that troubles you, you can also consider the equivalent automaton A∃({a},q,!b&b&next(q),G q).
Note that for any safety automaton A∃(Q,I,R,G phi) we can also consider the equivalent automaton A∃(Q,I&phi,R&phi,true).
About your second question: The automaton considered in the first question was FGa = А∃({p},!р,р->a&next(p),Fp). This automaton looks as follows:
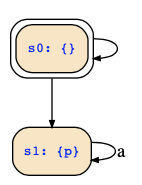
Hence, it may stay in its initial state as long as wanted, but if it should decide at some time to switch to state {p}, then it must be the case that from that point of time onwards, "a" must hold, since otherwise the self-loop on {p} which is the only transition, cannot be taken. If we change the acceptance condition from Fp to FGp, then the automaton will still accept the same words, namely the words that satisfy FGa.