Simplex Algorithm doubt ?

Question

In the exam question for 2022.02.16, I pivoted with x1. I used the logic that I need to reduce y0 from 0 to -1 hence in order to do that I need to reduce x1 (y0=5x0=4x1). Is the following approach and solution correct ?

After Pivotting X1, resulting constraints values are within the limits.

Answer 1

Your solution looks plausible to me. If we consider the geometry of the problem, we can rewrite the constraints as follows:

•       5*x0 - 4*x1 ≤ -1
•      -3*x0 + 7*x1 ≤  5

and thus also as

•     x1 ≥ 1/4 + 5/4*x0 (blue)
•     x1 ≤ 5/7 + 3/7*x0 (red)

Hence, solutions are above the blue and below the red line below:

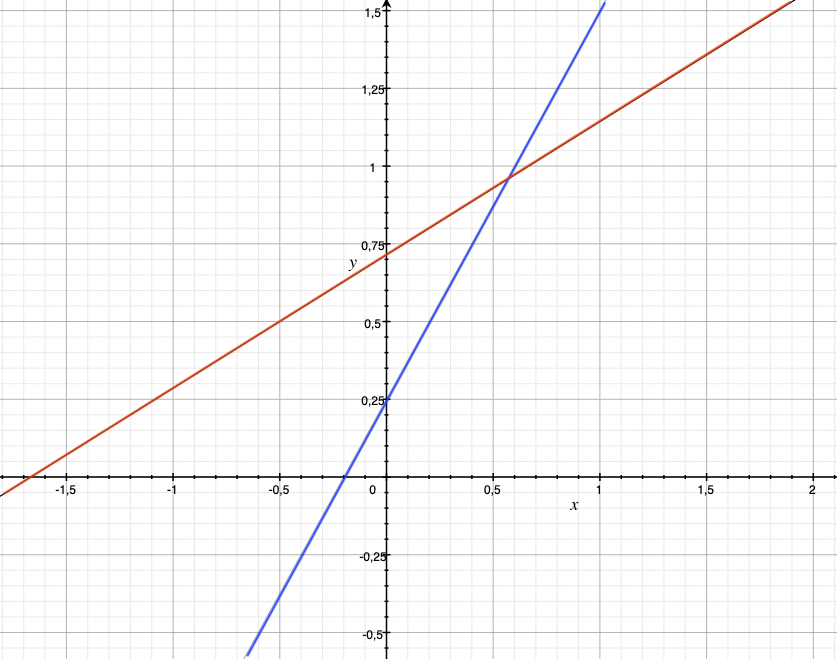
The simplex algorithm starts in (x0,x1) = (0,0) and moves to one of the intersection points. The example solution moves to (x0,x1) = (-1/5,0) and your solution moves to (x0,x1) = (0,1/4) which are both valid solutions.