The full solution is computed below, but let's directly address your question: B := attractor(0,winA0) := attractor(0,{s3,s4,s5,s6,s7}) := {s0,s3,s4,s5,s6,s7} as given in the example solution is correct. State s2 is controlled by player 1 which can can choose the transition s2->s1 so that we do not have to go to {s3,s4,s5,s6,s7}. However, s0 belongs to the attractor since s0 is controlled by player 0 who can choose the transition s0->s3 which enters the desired set. The states s1,s2,s8 are controlled by player 1, and player 1 can choose to stay there: s8->s1<->s2.
Let's see whether we agree with the solution, the outgoing colored edges show the choices of the players in the states. We therefore have the following plays:
- s0 -> s3 <-> s4 where player 0 wins with rank 8
- s1 <-> s2 where player 1 wins with rank 7
- s2 <-> s1 where player 1 wins with rank 7
- s3 <-> s4 where player 0 wins with rank 8
- s4 <-> s3 where player 0 wins with rank 8
- s5 -> s6 -> ... where player 0 wins with rank 8 as explained below
- in s6, player 1 has choices, but will lose the game with any choice:
- s6 <-> s5 where player 0 wins with rank 4
- s6 <-> s7 where player 0 wins with rank 6
- s6 -> s4 <-> s8 where player 0 wins with rank 8
- s6 -> s8 <-> s4 where player 0 wins with rank 8
- s8 -> s1 <-> s2 where player 1 wins with rank 7
So, the computation of the winning strategies is correct.
I do not understand your doubt 2, but maybe the above games answer that?
Here is the full computation of the winning strategies:
player0 0,3,5,7;
player1 1,2,4,6,8;
ranks 0:9; 1:6; 2:7; 3:8; 4:5; 5:3; 6:4; 7:6; 8:1;
transitions
0->3; 0->8; 1->0; 1->2; 2->1; 2->7; 3->2; 3->4;
4->3; 5->6; 6->3; 6->4; 6->5; 6->7; 7->6; 8->0; 8->1;
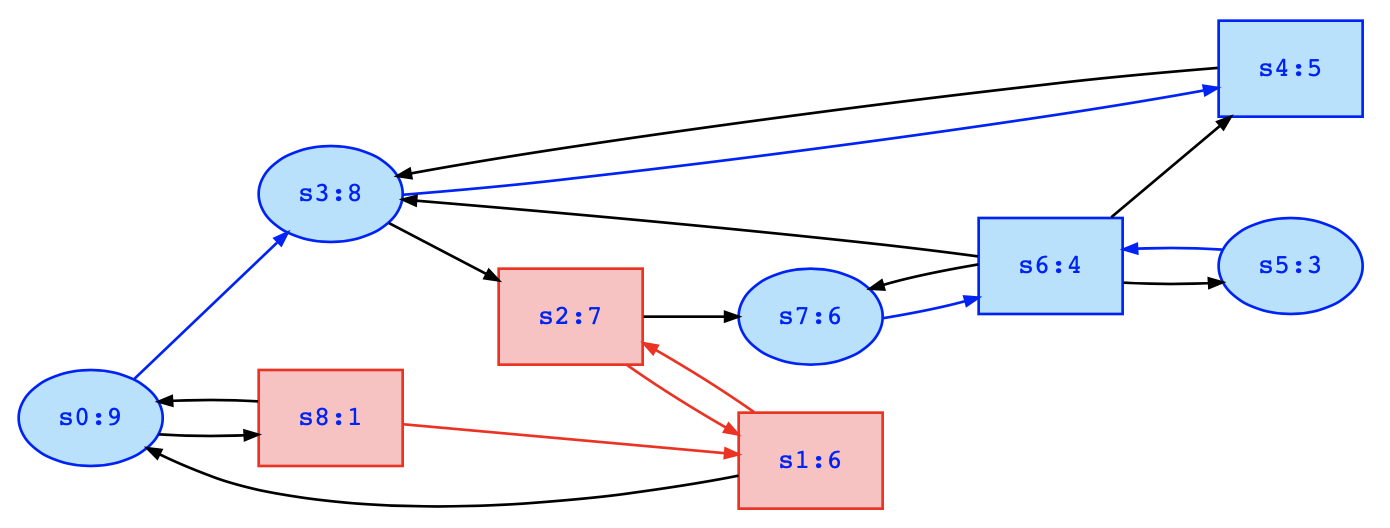
For the game graph, we find the highest rank h:=9 on states Qh:={s0}. As 9 is an odd number, player 1 may win if infinitely often visiting state s0 can be enforced by player 1, so we have i:=1. So, we compute the attractor set of player 1 and state s0 which are the states A := attractor(1,{s0}) := {s0,s1,s2,s8}. We remove these states from the game 0, and obtain game1 below which has the solution winA0={s3,s4,s5,s6,s7}; winA1={} as explained below.
Since winA0 is not empty, we have to solve another game that is obtained by removing the states B := attractor(0,winA0) := attractor(0,{s3,s4,s5,s6,s7}) := {s0,s3,s4,s5,s6,s7} from the game 0 which yields game 4 below which has the solution winB0={}; winB1={s1,s2,s8}. The solution of game 0 above is therefore win0={s0,s3,s4,s5,s6,s7}; win1={s1,s2,s8}.
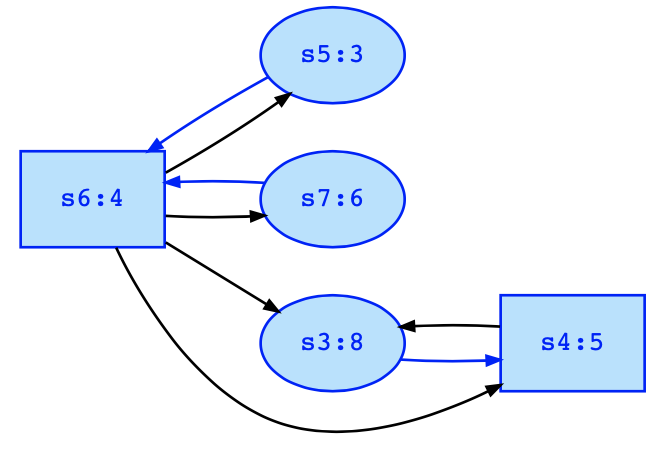
Now, we remove the states {s0,s1,s2,s8} from the game graph, and solve the remaining game 1 shown above. In that game, the highest rank is h:=8 on states Qh:={s3}. As 8 is an even number, player 0 may win if infinitely often visiting state s3 can be enforced by player 0, so we have i:=0. So, we compute the attractor set of player 0 and state s3 which are the states A := attractor(0,{s3}) := {s3,s4}. We remove these states from the game 1, and obtain game2 below which has the solution win0={s5,s6,s7}; win1={} as explained below. Since win1={} holds, it follows that we do not need the second recursive call, and the solution of game 1 is win0={s3,s4,s5,s6,s7}; win1={}, i.e., player 0 has a winning strategy in all states of this game.
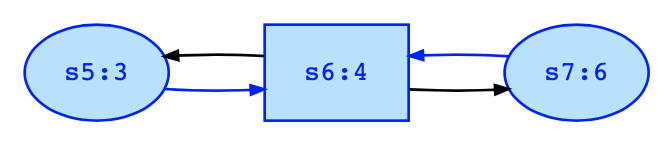
Now, we remove the states {s3,s4} from game 1 and solve the remaining game 2 shown above. Clearly, player 0 has a winning strategy in every state, since if player 1 will only finitely often visit state s7, it must visit state s5 from some time on always, but that implies that also state s6 is visited always from some time onwards. Therefore the highest rank that appears infinitely often would be 4, and player 0 wins. Otherwise, player 1 must visit s7 with rank 6 infinitely often, so that player 0 will win with rank 6. Hence, the solution of game2 is easily seen as win0={s5,s6,s7}; win1={}.

The above game 4 has clearly the solution win0={}; win1={s1,s2,s8} since there is only one infinite path where player 1 will win with rank 7.